车辆系统仿真：连续时间系统的数学模型

1.常用的数学模型

连续系统模型形式可以分为3类：连续时间系统模型、离散时间系统模型和混合模型（计算机控制系统模型）。常用的连续时间系统数学模型有以下4种。

1）微分方程

设系统的输入为u（t），输出为y（t），它们之间的关系即系统的微分方程为

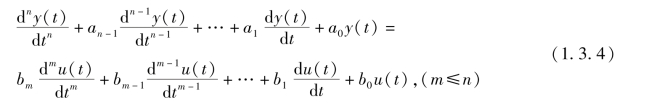
其中，ai（i＝0，1，…，n－1），bj（j＝0，1，…，m）为常系数。

若引进微分算子，则式（1.3.4）可以写成

pn y＋an－1 pn－1 y＋…＋a1 py＋a0 y＝bm pm u＋bm－1 pm－1 u＋…＋b1 pu＋b0 u

即

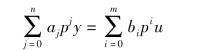
其中，an＝1，于是上式可写成下面形式

2）传递函数

对式（1.3.4）两边取拉普拉斯变换，并假设y（t）和u（t）及其各阶导数的初值均为零，则可得

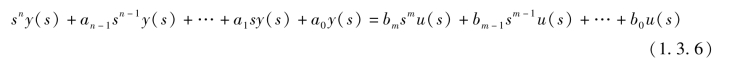
设

为系统的传递函数，则有

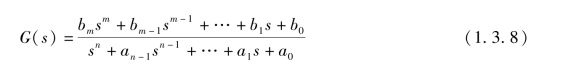
可见，在初值为零的情况下，用算子p所表示的方程与传递函数G（s）在形式上是等价的。

3）状态空间表达式

对于一个连续系统来说，微分方程和传递函数仅仅描述了系统的外部特性，即仅仅确定了输入量u（t）与输出量y（t）之间的关系，一般称为系统的外部模型。

为了描述系统的内部特性，引入状态变量。动态系统的状态变量是指能完全描述系统行为的最小一组变量，用向量X表示。系统的状态变量不一定具有严格的物理意义，线性时不变系统的状态空间表达式由状态方程和输出方程组成，即

式中　X——n维状态向量，X＝［x1，x2，…，xn］T；

U——r维输入向量；

Y——m维输出向量；

A（n×n）——系统矩阵；

B（n×r）——输入矩阵；

C（m×n）——输出矩阵；

D（m×r）——直传矩阵。

可见，状态方程是一阶微分方程组，非常适合用计算机求其数值解，因此，如果一个物理系统是用状态空间表达式来描述的，则可以直接利用状态方程编制积分求解程序对该系统进行仿真。

4）结构图表示

结构图是系统中每个元件或环节的功能和信号流向的图解表示，它比较直观，对单输入单输出线性系统可通过结构图变换很容易得出整个系统的传递函数；而对多输入多输出或具有非线性环节的系统也可通过面向结构图的仿真方法得到系统的动态特性。图1.3.1为一单输入单输出线性系统的结构图。

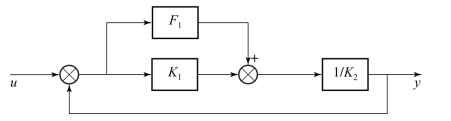
图1.3.1　单输入单输出线性系统的结构图

2.实现问题

在控制理论中，实现问题是指由微分方程或传递函数确定系统的状态空间表达式，由于状态空间模型易于在计算机上实现对系统的仿真，因此实现问题对于计算机仿真技术有实际的意义。对一个连续系统进行仿真，首先要建立系统的内部模型——状态空间表达式。

1）化微分方程为状态方程

设系统的微分方程如式（1.3.4），先设系统不含输入量的导数项，即

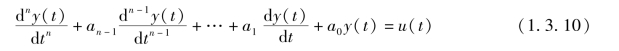
引入状态变量

则有

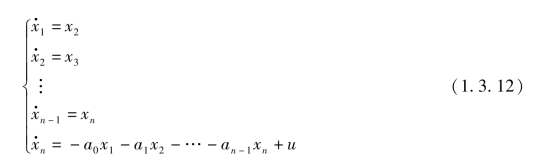
把式（1.3.10）的微分方程写成矩阵形式

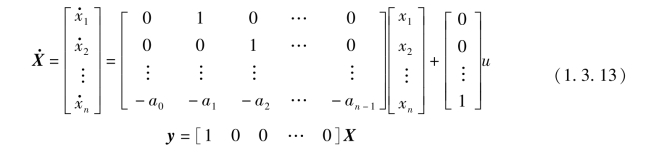
简写成

若系统中含有输入量的导数（一般输入导数项的次数小于或等于系统的阶数n，即m≤n），这里以m＝n为例说明。系统微分方程如式（1.3.4）所示，其中m＝n。

取状态变量

x1＝y－β0 u

xi＝xi－1－βi－1 u（i＝2，…，n）

可以推出（读者可以自己推导）

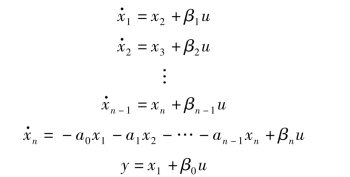
则同样可得如下状态空间模型：

式中

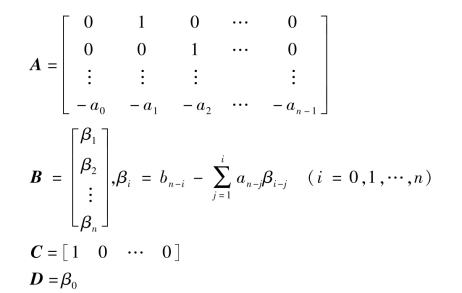
选取的状态变量不同，所得到的状态方程也不一样，即转换方程不唯一。

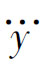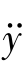例：设系统微分方程为＋6＋11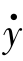＋6y＝6u，其中y为输出量，u为输入量，试求系统的状态空间表达式。

解：选取状态变量为x1＝y，x2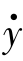＝，x3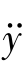＝，并将x1，x2，x3代入原方程，得

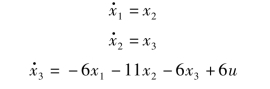
用矩阵形式表示，则可写成

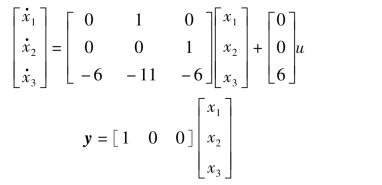
2）化传递函数为状态方程

对于一个可实现的传递函数或传递函数矩阵其实现也是不唯一的，根据控制理论可分别给出可控标准型、可观标准型和对角型等。这里根据仿真的要求，仅列举可控标准型的建立。

设系统传递函数为

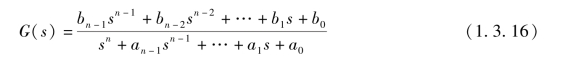
将式（1.3.16）改写成(https://www.xing528.com)

将

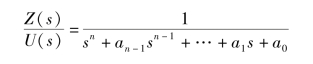
和

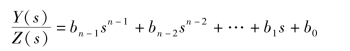
取拉普拉斯反变换，可得

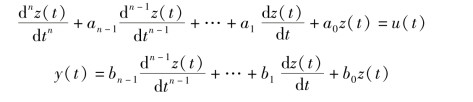
取状态变量为

x1＝z1，x2＝z·，…，xn＝z（n－1）

便可得到可控标准型

式中

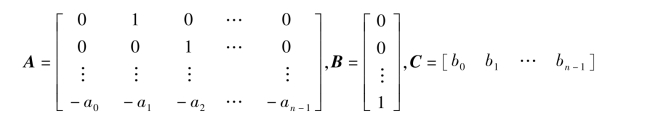
3）化系统结构图为状态方程

设一个一般系统的结构如图1.3.2所示，其中每个环节的传递函数Gi（s）（i＝1，2，…，l）可用多项式表示，也可用零极点表示，即

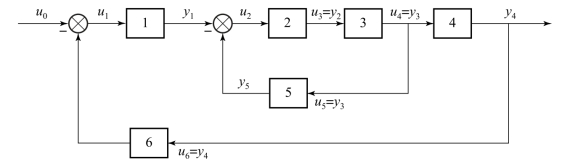
图1.3.2　一般系统的结构图

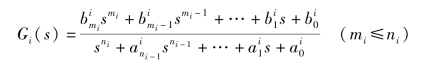
或

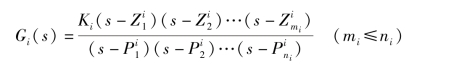
各个方块之间的联结方式可用一个连接矩阵Z来表示

其中，每一个元素Zij（i＝1，2，…，l；j＝1，2，…，l）表示各环节之间的联结关系，l为方块数。当Zij＝K时，则表示第j方块的输出乘以K之后再输入到第i环节中去。所以，Zij＝1表示直接联结，Zij＝0表示不联结，负号则表示负输入。对于图1.3.2所示的系统容易写出

可用计算机程序实现转换，其算法步骤归结如下。

（1）输入方块数l以及各块传递函数Gi（s）的参数。对于多项式输入ai（i＝1，2，…，ni），bj（j＝1，2，…，mi）；对于零极点输入Pi（i＝1，2，…，ni），Zj（j＝1，2，…，mi）。

（2）输入连接矩阵元素Zij（i＝1，2，…，l；j＝1，2，…，l）。

（3）若Gi（s）为零极点输入，则需通过子程序变换成多项式形式。

（4）将全部Gi（s）变换成状态空间，并用可控标准型表示为

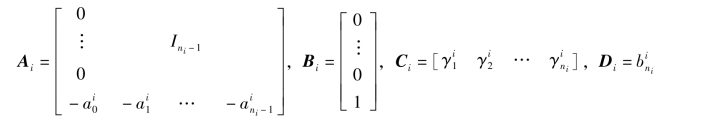
其中，。

（5）由Ai，Bi，Ci，Di（i＝1，2，…，l）组成4个对角块阵

并组成系统

式中，X＝［x1x2…xi］T，Y＝［y1y2…yi］T，xi＝［xi1xi2…xin］T（i＝1，2，…，l）。

（6）式（1.3.21）中输入量U包括参考输入和交连输入两部分，即

带入式（1.3.21），经整理后可得

其中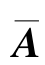，＝A＋BZ（I－DZ）－1C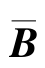，＝B＋BZ（I－DZ）－1D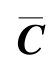，＝（I－DZ）－1C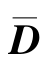，＝（IDZ）－1D。

如果系统中加入了非线性环节，则由于非线性环节只是在两个线性环节之间起变换作用，即将一个线性环节的输出经过非线性变换作为另一个线性环节的输入，且由数字计算机特有的逻辑功能实现起来很容易；因此，只需在上述线性结构图基础上，在每两个相邻的线性环节之间串接一个F（Zij）环节，使

而

其中，Zij表示假定没有加入非线性环节时系统连接矩阵的元素。这里重新定义Zij的标号以代表不同的非线性类型。

其算法步骤前5步同线性结构完全相同，得

输入向量　

其中，u0为参考输入，F（Zij）Y为交连输入，且

可假设F（0）表示线性环节i和j之间不联结；F（1）为直接联结；Zij为其他标号时F（Zij）表示i和j之间有某种类型的非线性联结。

3.系统状态初始值设置

如果系统是非零初始条件，那么从外部模型（传递函数等）变换到内部模型（状态方程）还必须考虑如何将给定的初始条件——通常是给定输入u（t）、输出y（t）及其各阶导数的初始值——转变为相应的状态变量的初始值。

设系统的微分方程如式（1.3.4）所示（式中m＝n－1），并设它的状态空间模型为

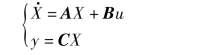
式中　A——n×n矩阵；

B——n×1矩阵；

C——1×n矩阵。

已知系统的初始条件为

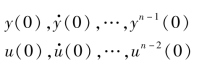
则为了由上述初始值求出状态变量x1，x2，…，xn的初始值，可列出以下方程

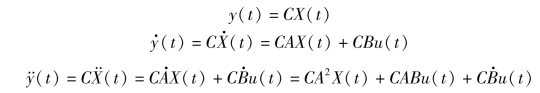
于是可得下列矩阵方程

式中

由式（1.3.29）可得

即，若V－1存在，则可由式（1.3.30）求出X（t）的初始值。由控制理论可知，V矩阵是系统（A，B，C）的可观判别阵，若V非奇异，则（A，B，C）是完全可观的。也就是说，由外部输入输出的初始值转变为内部状态变量初始值的条件是，系统（A，B，C）是完全可观的。