车辆系统数学模型及表达形式简介

系统模型的表达形式有很多，如数学方程式、图、表等，其中数学方程式是系统模型最主要的表示方式。系统的数学模型就是对系统与外部的作用关系及系统内在的运动规律所作的抽象，并将此抽象用数学的方式表示出来。

从系统学的角度，一个系统可以被定义成下面的集合结构：

式中　T——时间集；

X——输入集；

Ω——输入段集；

Q——内部状态集；

Y——输出集；

δ——状态转移函数；

λ——输出函数。

它们的含义与限制如下。

1）时间集T

T是描述时间和为事件排序的一个集合。通常，若T为整数集Z或实数集R，则S称为离散时间系统或连续时间系统。

2）输入集X

X代表界面的一部分，外部环境通过它作用于系统，而系统不直接控制集合X。通常取X＝Rn，其中n∈Z＋，即X代表n个实值的输入变量。还有一种常用的X，即X＝Xm∪∅，其中Xm是外部事件的集合，∅是空事件。

3）输入段集Ω

输入段集是这样一个映射，ω：〈t0，tf〉→X，其中，〈t0，tf〉是时间集中从t0（初始时刻）到tf（终止时刻）的一个区间。所有上述输入段所构成的集合都记作（X，T），输入段集Ω是（X，T）的一个子集。一个输入段描述了在某时间间隔内系统的输入模式，当系统嵌套在一个大系统中时，上述模式由系统的环境所决定。当系统处于孤立的情况时，环境被一个段集所替代。考虑到重构，该段集应该包括作为大系统的一个组成部分的S所能接收到的所有模式。

当T＝R，X＝Rn时，Ω为分段连续段集，若Ω为Xm（外部事件集）上的离散事件段集，则ω：〈t0，tf〉→Xm∪∅，并且除对于有限的事件时间集合｛τ1，…，τn｝⊂〈t0，tf〉以外，均使ω（t）＝∅。最后，在T＝Z时，Ω是一个有限序列集。

4）内部状态集Q

内部状态集Q表示系统的记忆，即过去历史的遗留物，它影响着现在和将来的响应，是内部结构建模的核心。例如，对于线性系统

X为状态集，是系统建模的核心。

5）状态转移函数δ

状态转移函数是一个映射δ：Q×Ω→Q，它表示若系统在时刻t0处于状态q，并且施加一个输入段ω：〈t0，tf〉→X，则δ（q，ω）表示系统在tf的状态。因此，任意时刻的内部状态和从该时刻起的输入段唯一地决定了段终止时的状态。

对于每一个在q∈Q，ω∈Ω，t在ω的定义域中

δ（q，ω）＝δ［δ（q，ωt＞），ω＜t］　　（半群公理）

其中，（由t0到t的ω部分），（由t到tf的ω部分）。

对于任意时刻t的状态q1＝δ（q，ωt＞）都应概括以前必要的历史情况，这是为了从该状态起继续实验，能和其他情况一样最终得到相同的终态。

根据给定的状态定义可知，状态集的选择不是唯一的，甚至其维数也是不固定的。因此，寻找系统的一个合适而有利的状态空间是一件很有意义的事。一旦找到了这样的状态空间，它将使我们能用当前的一个抽象的数值去替代过去的数值。这种内部结构的形式也大大简化了处理分解（内部结构的具体化）和仿真（和其他系统的关系）的技能。

状态集合是一个建模概念，在真实系统中并没有什么东西和它直接对应。另外，输入段集、状态集和状态转移函数这三者共同表示一个状态段集。

6）输出集Y

输出集Y代表着界面的一部分，系统通过它作用于环境。除方向不同外，输出集的含义和输入集完全相同。如果系统嵌套在一个大系统中，那么，该系统的输入（输出）部分恰是其环境的输出（输入）部分。

7）输出函数λ

输出函数的最简单形式是映射λ：Q→Y。它使假想的系统内部状态与系统对其环境的影响相关联。但是，上述的输出映射不允许输入直接影响输出，因此更为普遍的一个输出函数是下面的一个映射λ：Q×X×T→Y。换言之，即当系统处于状态Q时，并且系统的当前输入是X时，λ（Q，X，T）能够通过环境检测出来。进一步讲，输出函数，并不一定是时不变的，通常是一个多对一的映射，因此，状态常常不能直接观测到。

根据上面提出的形式化的定义，一个系统的行为是其内部结构的外部表现形式，即在叉积（X，Y）×（Y，T）上的关系。

这个关系可作如下计算，对于每一个状态q∈Q和在Ω中的输入段ω：〈t0，tf〉→X存在一个相关联的状态轨迹

STRA Jq，ω：〈t0，tf〉→Q

使得

STRA Jq，ω（t0）＝q

和对t∈　〈t0，tf〉，有

STRA Jq，ω（t0）＝δ（q，ωt＞）

上述的状态轨迹是一个可检测的结果，或者可在计算机仿真过程中被计算出来。这个轨迹的可观测投影是和q∈Q，ω∈Ω相关的输出轨迹，即

OTRA Jq，ω：〈t0，tf〉→Y

例如，使用简单的输出函数形式λ（q），则存在(www.xing528.com)

OTRA Jq，ω（t）＝λ（STRA Jq，ω（t））

这时，系统的行为就可以通过输入－输出关系Rs表现出来，即

每一个（ω，ρ）∈Rs的元素称为输出段对，它表示一个有关系的实验结果或观测结果，在该系统中，ω是系统的输入，ρ是观测到的输出。由于一个系统在初始时刻能处于任意一个状态，因此对于同一个输入段ω可对应多个输出段ρ。

从上述系统学的观点可以描述我们所熟悉的数学模型形式。

1）时不变连续时间集中参数模型

M1：（U，X，Y，f，g）

式中　u∈U——输入集合；

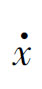＝f（x，u），x∈X——状态集合；

y＝g（x，u），y∈Y——输出集合；

f——函数的变化率，满足利普希茨的条件；

g——输出函数。

这样的模型形式是由式（1.3.1）定义的集合结构的特殊情况。

事实上，M1＝S1，且

式中　t∈T——⊂R；

X≡U——Rm，m∈Z＋；

Q≡X——Rn，n∈Z＋；

Y≡Y——Rp，p∈Z＋；

Ω——｛ω：［t0，t0＋τ］→U处处连续的函数，τ＞0｝；

δ——假定微分模型具有唯一解Φ（t），满足

Φ（0）＝q0

dΦ（t）／d t＝f（Φ（t），ω（t））

则映射δ：Q×Ω→Q能在解Φ（t）已知的情况下被确定。

2）离散事件系统模型

在某些情况下，特别是在制造系统、计算机网络系统、信息管理系统的研究中，真实世界的过程能看作是由一组事件所构成，而这些事件是在特定的时间点上发生变化的。可以给出离散事件模型M2的公式来作为该系统的数学描述，即

M2：（Xm，Sm，Ym，δm，λm，τm）

式中　Xm——外部事件集合；

Sm——序列离散事件状态集合；

Ym——输出集合；

δm——准转移函数；

λm——输出函数，λm：Sm→Ym；

τm——时间拨动函数，它也是一个映射τm：Sm→R0，τm：，说明系统在没有外部事件作用下，在一个新的转移发生之前它将在状态S下保持多长时间。

准转移函数可以用以下两种方式之一来描述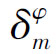：，映射Sm→Sm，这说明，假如没有外部事件发生，系统也将从一个给定状态进展到另一个状态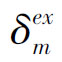；，映射Xm×Sm×T→Sm，它说明，假如系统处于状态S，同时在上一个状态转移发生后的时间e有一个外部时间X，则将发生上述转移。

可以证明：M2≡S2，且

式中　T——⊂R；

X——Xm∪∅；

Ω——：〈t0，t1〉→X，ω（t）≠∅对（t0，t1）的大部分有限子集｝，为离散时间段集；

Q——从顺序集合Sm及时间拨动函数τm构造出来的实际状态集合，即

因此一个合成的状态是（s，e）对，其中s是一个顺序状态，而e是在这个状态下停留的时间；

δ——由δm构造而得，即映射Q×Ω→Q，对每个τ，状态可从以下获得：

前面给出了一个将系统看作为集合结构的一般定义，在实际情况下，人们是永远不会从这样一个一般结构出发的，而是采用一个更加特殊的“模型形式”。