水文测验误差分析及评定：目估定线二次插值推流结果

目前，有部分水文站未采用数学模型拟合水位流量关系曲线，而采用目估定线且用拉格朗日二次插值公式推算流量。在插值结点，推算流量等于从关系线上查读的流量，其误差等于目估线推算误差。在计算点，推算流量由插值公式计算，其误差包括目估线推算误差和插补误差。

（一）目估线推算误差

过去，流量资料整编采用目估定线、人工推流，推算值的误差称为目估线推算误差。关系线标准差仍用式（11-3-6）计算。现在的问题是，水位流量关系未用数学模型模拟而采用目估定线，目估线推算误差标准差如何计算。

第一种处理方法是仍采用式（11-4-2）计算。这样做的前提是，假定目估确定的关系线与数学模型模拟的结果一致。

第二种处理方法是采用式（11-4-2）的平均值。用式（11-4-2）计算的目估线推算误差标准差随水位而变。作为一种简便的近似方法，可取

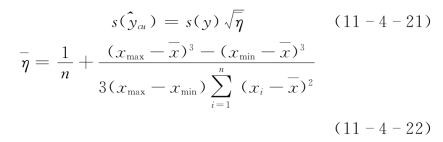
式中：xmax，xmin分别为用于推算流量的最大、最小有效水位的对数值。

第三种处理方法是取η等于其最小值。由式（11-4-2）知，η的最小值为

由此得目估线推算误差标准差为

例11-4-2 哈尔滨站2002年畅流期资料见表11-4-1。测次n=17，人工定线推流，曲线查得流量见表11-4-1。试评定曲线推算值误差。

表11-4-1　哈尔滨站2002年畅流期实测流量表

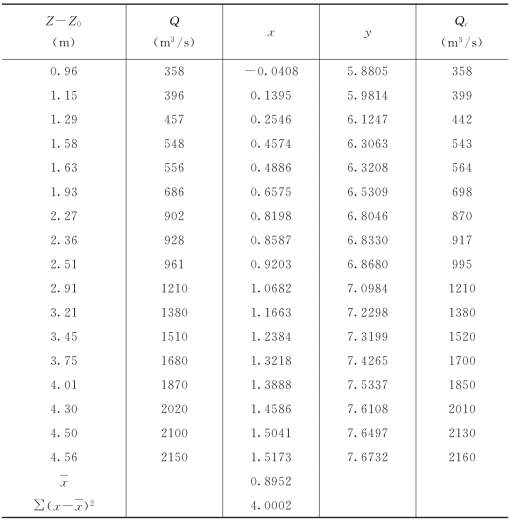
解：

（1）关系线标准差为

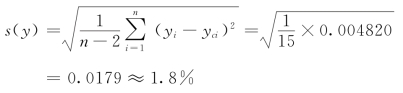
（2）推算值标准差。最大流量标准差为

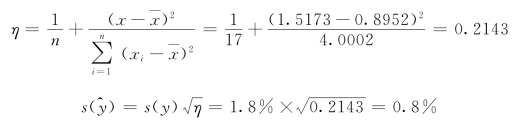
最小流量标准差为

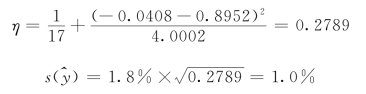
最小标准差出现在Z-Z0=2.45m处，x=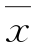=0.8952，则

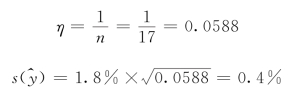
按式（11-4-22）计算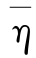，得(www.xing528.com)

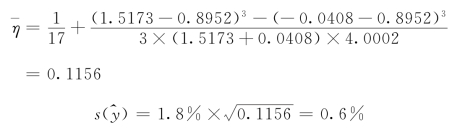
为保险起见，推算值标准差可取=1.0%，但取=0.6%更合理些。

（二）二次插值的推算值误差

用二次插值求得的推算流量为

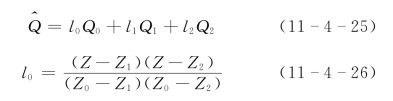
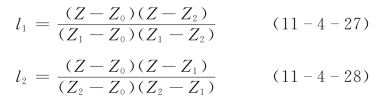
式中：Z为计算水位；Z0，Z1，Z2分别为插值结点水位；Q0，Q1，Q2分别为相应的结点流量。

二次插值推算误差由两部分组成，一部分是由人工线推算误差引起的，因为结点流量是从人工线上查读的值，带有人工线推算误差；另一部分是由插值本身引起的插值误差。对式（11-4-25）应用标准差传播律，并假定推算流量和各结点流量相等，得

式中：为人工线推算误差引起的误差标准差。

显然，当Z=Zi，i=0，1，2时，有，而当Z取其他值时，有。设步长为h，可以证明当Z=和时，最小，其值为

平均值可估计为

对每个计算点，插值误差是系统误差；对多个计算点，插值误差是可变系统误差。鉴于此，可采用下述方法计算插值误差标准差：计算所有计算点插值流量与人工线推算流量相对误差，其最大值为a+，最小值为a-，根据第二章第四节，假定插值误差服从均匀分布，则其标准差可估计为

这样，用人工定线且用二次插值推算流量时，推算值误差标准差为

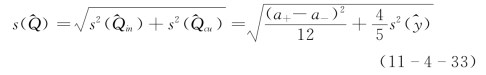
例11-4-3 根据表11-4-1资料确定哈尔滨站人工定线且用二次插值推算流量时的插值误差标准差和推算流量标准差。

解：采用一元三点等距插值，水位步长分别取h=0.05m、0.10m、0.20m，最大误差a+=0.7%，最小误差a-=-0.9%，于是插值误差标准差为

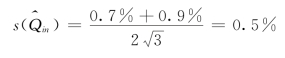
取=0.6%，推算流量标准差为

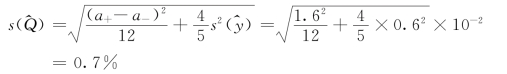
说明一元三点插值的推算流量误差标准差大于人工定线推流的推算流量误差标准差。