水文测验误差分析：关系曲线检验

检验两条关系曲线仍用t检验。这里所说的t检验是指在两个正态总体方差未知但却相等的条件下，检验两个总体均值是否相等。为了判断相邻年份或相邻时段的水位流量关系曲线是否发生明显变化，需进行该项检验。在t检验中，假设σ21=σ22，意味着原来用以确定水位流量关系的实测点的离散程度与校核流量点的离散程度一致。如果由于测验误差等影响，两者的离散程度不一致，就不能假定σ21=σ22，否则就会得出错误的推断。因此，在作t检验之前，应当首先对两个正态总体方差相等这一假定是否成立进行检验，也就是说首先要进行F检验[55，56]。

有关F检验和t检验的方法已在第一章叙述，这里以两个算例予以说明。

例11-3-4 检验相邻年份水位流量关系是否发生显著变化，数据取自文献[56]。四川省油房沟水文站1981年实测点n1=25，对本年水位流量关系曲线的平均偏差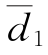=0.7%，偏差方差s21=25.3×10-4；1982年实测点n2=20，对1981年水位流量关系曲线的平均偏差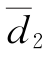=2.2%，偏差方差s22=22.8×10-4。取显著性水平α=0.05。

解：

（1）F检验。

假设H0∶σ21=σ22

统计量为

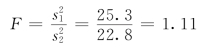
由显著性水平α=0.05，ν1=n1-1=24，ν2=n2-1=19，查F分布表得临界值Fα/2（ν1，ν2）=2.45。由于F＜Fα/2，故接受原假设，认为两年流量实测点对1981年水位流量关系曲线的离散程度无显著差异。

（2）t检验。

假设H0∶μ1=μ2

统计量为

(www.xing528.com)

因为

所以

由α=0.05，n1+n2-2=43，查t分布表得临界值tα（n1+n2-2）=2.02。因为＜t0.05（43），所以接受原假设，认为两年的水位流量关系没有发生显著变化。

例11-3-5 检验相邻年份水位流量关系是否发生显著变化。哈尔滨水文站2001年实测点n1=17，对本年水位流量关系曲线（人工定线）平均偏差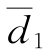=0.3%，偏差方差s21=4.1×10-4；2002年实测点n2=17，对2001年水位流量关系线平均偏差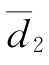=4.2%，偏差方差s22=39.6×10-4。取显著性水平α=0.05。哈尔滨站2002年畅流期实测流量成果见表11-4-1。

解：首先进行F检验。

假设H0∶σ1=σ2

统计量为

由显著性水平α=0.05，ν1=n1-1=16，ν1=n2-1=16，查F分布表得临界值Fα/2（ν1，ν2）=2.77，由于F＞Fα/2，故拒绝原假设，认为两年流量实测点对2001年水位流量关系曲线的离散程度有显著差别。

这样，t检验的前提被否定了，也就不能作t检验了。由此可知，两年的水位流量关系发生了显著变化。