SL247—1999《水文资料整编规范》规定，关系曲线为单一曲线、使用时间较长的临时曲线及经过单值化处理的单一线，且测点在10个以上者，应作符号检验、适线检验和偏离检验。
（一）符号检验
符号检验的实质是用样本资料检验H0：P=0.5这个假设能否被接受，判定关系线定得是否存在系统偏离。检验可采用以下两种方法中的任意一种。两种方法均为双侧检验。
第一种方法是利用近似的U检验法。统计实测点与关系曲线的偏差的正负号个数（偏离值为零者，作为正负号测点各半分配）。正偏差个数记为n+，负偏差个数记为n-。统计量为
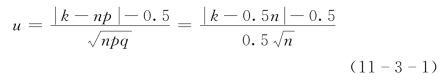
式中：n为测点总数；k为正号或负号个数，可取k=n+。
计算u值。按给定的显著性水平α，由正态分布表查得临界值u1-α/2。若u＜u1-α/2，则接受假设H0，认为关系曲线无显著系统偏离，定线合理；否则，则拒绝假设H0，认为曲线定得不合理。
第二种方法是查表检验法。检验时，取r=min（n+，n-），即正号个数和负号个数的较小者。按给定的显著性水平α，由符号检验表查得临界值rα，若r＞rα，则接受假设H0，认为曲线无显著系统偏离，定线合理；否则，则拒绝假设H0。
例11-3-1 哈尔滨水文站2001年畅流期资料见表11-2-1。按一阶曲线拟合结果，测点数n=17，偏差正号9个，偏差负号8个，于是n+=9，n-=8。取显著性水平α=0.25。问选配的曲线是否存在系统偏离？
解：第一种方法，按k=9，统计量为
由显著性水平α=0.25，查正态分布表得临界值u1-α/2=1.15。由于u＜u1-α/2，故接受假设H0，认为曲线无显著系统偏离。
第二种方法，r=min（9，8）=8，由显著性水平α=0.25查符号检验表得临界值rα=5，由于r＞rα，故接受假设H0，认为曲线无显著系统偏离。
（二）适线检验
适线检验的目的是检验实测点在曲线两侧的排列情况，测点分布是否均衡。有时，尽管关系曲线通过了符号检验，表明所定曲线无显著系统误差，但在某水位级有连续偏大或连续偏小的情况，说明所定曲线与测点配合不好。
将n个测点按水位递增顺序排列，计算实测值与关系曲线的偏差。从第二个测点开始，统计偏差正负号变换次数。相邻两测点偏离曲线同符号的记为“0”，不同符号的记为“1”。设“0”的个数为n0，“1”的个数为n1，n0+n1=n-1。显然，n1越大，测点分布越均衡。
适线检验仍应用符号检验原理。在符号检验中，统计量采用式（11-3-1），属双侧检验，n+太大或太小都不会通过检验，说明定线不合理。在适线检验中，n1越大越好。实际工作中，只要k=n1＞0.5（n-1），就认为合理，不必检验，只在k＜0.5（n-1）时检验。统计量为
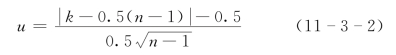
由实测资料计算u值，按给定的显著性水平α，由正态分布表查得临界值u1-α。若u＜u1-α，则接受原假设，认为定线合理；否则，则拒绝原假设。
例11-3-2 哈尔滨站2001年畅流期资料见表11-2-1。由一阶曲线拟合结果，计算偏差d1=y-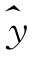
，见表11-2-1。测点数n=17，n1=8，n0=8，即k=8，按式（11-3-2）得u=-0.25，取显著性水平α=0.05，由正态分布表查得临界值u1-α=1.96，u＜u1-α，说明一阶曲线通过适线检验，实测点在曲线两侧分布是均衡的。
（三）偏离数值检验
偏离数值检验的目的是检验实测点对关系曲线有无系统偏离。可以说，符号检验是定性检验有无系统偏离，而偏离数值检验是从数值上进一步检验有无系统偏离。设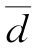
为n个测点相对偏差的平均值，s为相对偏差标准差，则
服从自由度ν=n-1的t分布。现检验假设H0：μd=0。在H0为真的条件下，有
给定显著性水平α，由t分布表查得临界值tα（n-1）。若
＜tα（n-1），则接受原假设，认为测点对关系曲线无显著系统偏离；否则，则拒绝原假设。偏离数值检验也是t检验，是成对出现的数值比较[55]。
例11-3-3 哈尔滨水文站2001年畅流期资料见表11-2-1。对于一阶曲线n=17，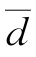
=0.0%，s=2.2%，取显著性水平α=0.10。试问关系曲线可否通过偏离数值检验？(www.xing528.com)
解：假设H0∶μd=0。由ν=n-1=16，α=0.10，查t分布表得临界值t0.10（16）=1.746。统计量为
由于
＜tα（n-1），故接受假设H0，认为所定关系曲线无显著系统偏离。实际上，由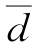
=0.0可直接看出一阶曲线无系统偏离。
（四）偏离标准差检验
SL247—1999《水文资料整编规范》规定，稳定的水位流量关系曲线、临时曲线法的主要曲线及经单值化处理的单一线，均应计算关系点对关系线的标准差，即偏离标准差。
偏离标准差按下式计算
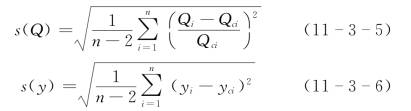
式中：Qi为实测流量；Qci为与实测流量Qi相应的曲线上查读流量；yi=lnQi，yci=lnQci；n为实测点总数。
事实上，上述两式所得结果是一致的。如令
则
将其展开为幂级数，得
略去高次项，得
ed≈1+d
即
通常用式（11-3-5）计算较方便。在曲线拟合中若水位和流量均取了对数，则用式（11-3-6）更方便。
应用m（m≥2）元线性回归或m（m≥2）阶正交多项式回归时，采用下式计算标准差
或
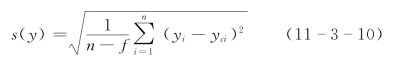
式中：f=m+1为待估计系数的个数。
（五）不反曲检验
根据水位流量关系曲线的性质，不反曲是指曲线的二阶导数大于零。关系曲线确定后，只要从线上读取的等水位间隔相应流量的差值是递增的，曲线便是不反曲的。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
