误差来源及计算方法-水文测验误差分析与评定

相应水位的误差来源，一是水位观测误差，二是用某种方法计算的相应水位与相应水位真值的误差，这项误差可称为代表性误差。于是，相应水位误差标准差可表示为

式中：s（Zmr）为相应水位代表性误差标准差；s（Zmm）为相应水位观测误差标准差。

假定流量测验过程中各部分瞬时水位观测误差标准差相等，根据标准差传播律，可求得各种相应水位计算方法的观测误差方差如下：

（1）首末平均法。该法的观测误差方差计算公式为

（2）多线平均法。该法的观测误差方差计算公式为

（3）bv加权法。该法的观测误差方差计算公式为

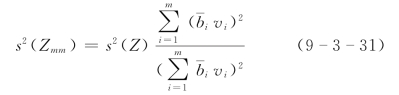
（4）部分流量加权法。该法的观测误差方差计算公式为

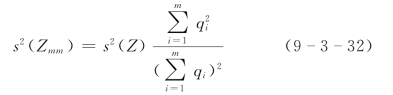
为了简化计算，将各种方法计算的相应水位观测误差标准差一律简化为多线平均法的形式。这样，相应水位误差标准差可写为

(www.xing528.com)

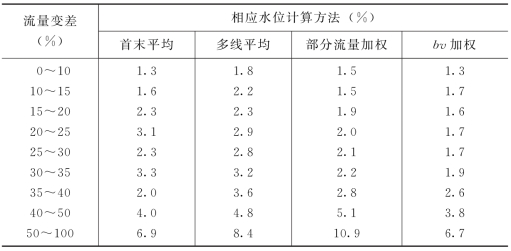
瞬时水位观测误差标准差的计算已在第一节介绍，关键是相应水位代表性误差标准差的确定。目前，尚未见到从理论上或通过实测资料确定相应水位近似真值的方法，这给计算相应水位误差标准差带来一定困难。早在20世纪70年代，为了对原流量测验规范的某些规定进行论证和改革，我国部分省（自治区、直辖市）水文机构曾做了大量试验分析工作。当时，黑龙江省水文总站采用模拟实测流量的方法对21个水文站的一次测流流量允许流量变差和计算相应水位的各种方法进行分析论证^[2]。经过多站综合，求得了一次测流流量变差与由于相应水位计算导致的流量误差标准差之间的关系，见表9-3-1。

从表9-3-1可以看出：①就相应水位计算精度而言，bv加权法优于部分流量加权法，部分流量加权法优于多线平均法，多线平均法优于首末平均法；②一次测流流量变差越大，相应水位的代表性误差越大，限制一次测流流量变差就是限制相应水位的代表性误差。

表9-3-1中的流量误差相对标准差可以转换为水位标准差。设某水文站的水位流量关系已通过回归分析建立起如下形式的经验公式

表9-3-1　一次测流流量变差与流量误差标准差关系表

式中：Z0为断流水位；C，β分别为已定参数。

由第一章可知，回归值Q的误差标准差由C，β的标准差决定。现在，我们将式（9-3-34）粗略地看作函数关系，目的是探讨流量与水位误差间的传递方式。对式（9-3-34）应用标准差传播律，得

式中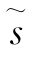：（Q）为表9-3-1中的流量误差标准差。

式（9-3-35）传递的是相应水位代表性误差与由此引起的流量误差，不包括流量和水位观测误差。因此，可用式（9-3-35）将表9-3-1中的流量误差标准差转换为相应水位代表性误差标准差。

【注释】

[1]姚永熙.浮子式自记水位计误差分析.水利电力部南京水利水文自动化研究所，1984

[2]黑龙江省水文总站.几项规范规定的试验分析报告（第一册）.1972