实测浮标流速误差及其分析

（一）上、下断面间距误差

行业标准SL58—93《水文普通测量规范》规定，在纵断面测量中，各横断面纵向距离应进行往返测量，不符值应小于1/500。又规定，使用交会法测定起点距时，所设基线长度的往返不符值应不大于1/1000。

上下断面间距由上中断面间距和中下断面间距组成。设上中断面间距为L，若用尺长为l的尺一段一段地丈量断面间距，已知钢尺的标准差为s（lr），则

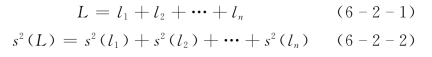
由于s（l1）=s（l2）=…=s（ln）=s（lr），故有

若s（lr）未知，则可通过对间距往返多次测量，按下列公式计算

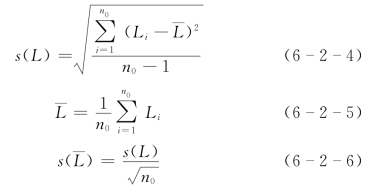
式中：n0为测回数，单尺一个往返为两个测回；Li为第i个测回的断面间距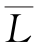；为断面间距平均值，即为最后取用的断面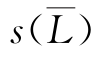间距；为断面间距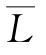的标准差。

若断面间距已确定，需重新检定其长度，则可应用不符值理论确定断面间距的标准差。设往测断面间距为L1，返测断面间距为L2，则

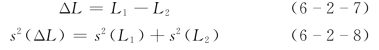
由于s（L1）=s（L2）=s（L），故有

通常，给出的不符值是an=s（ΔL）/L或an=2s（ΔL）/L，所以若断面间距测量误差符合其不符值规定，就可以继续使用原间距值，其标准偏差按式（6-2-9）计算。例如，按规定an=1/500，断面间距相对标准差为

对于中下断面同样有式（6-2-10），于是浮标上下断面间距标准差为

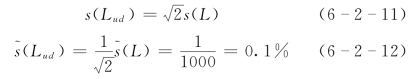
（二）记时误差

1.启动和停止停表所引起的误差

启动停表误差是由于持表人看到或听到信号与停表不一致所产生，与持表人使用停表的熟练程度有关。停止停表误差的产生原因也类似。浮标运行历时为

式中：tu，td分别为浮标通过上、下浮标断面时停表读数。

记时误差标准差为

因为一般取s（td）=s（tu）=s（t），所以

一般，启动和停止停表标准差s（t）=0.03s，对于水文观测取s（t）=0.06s，故有

2.停表本身的误差

国家标准GB50179—93《河流流量测验规范》规定，在检查停表时，应以每日误差小于5min带秒针的钟表为标准时，与停表同时走动10min，当读数差不超过3s，可以认为停表合格。这说明停表本身存在两方面误差：

（1）用于校正的时钟所产生的误差。24h不大于5min，那么反映在停表上，运行历时T（s），其误差Δt2应不大于a2（s），a2用下式求得

解得

Δt2可正可负，为随机误差，假定服从正态分布且a2为限差，则用于校正的时钟所产生的误差标准差为

（2）停表运行误差。要求停表运行10min，误差不超过3s，那么运行历时T（s），其误差Δt3应不超过a3，a3按下式计算

解得

Δt3可正可负，为随机误差，假定服从正态分布且a3为限差，则停表运行误差标准差为

3.停表读数误差

国家标准GB50179—93《河流流量测验规范》规定，浮标运行时间读数精确至0.1s，运行历时大于100s时，可精确至1s。由于读数误差服从均匀分布，故当运行历时不大于100s时，分布半宽a4=0.05，读数误差标准差为(www.xing528.com)

当运行历时大于100s时，分布半宽a4=0.5，读数误差标准差为

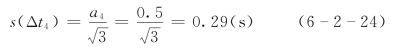
4.瞄准误差引起的运行历时误差

水面浮标通过上或下断面时，由于瞄准误差和观测员精神不集中或判断不准确，可能使浮标离开或未到断面线ΔL时才发出指令。如果不考虑观测员精神不集中或判断不准确导致的误差，那么ΔL仅由瞄准误差引起。瞄准误差由视差引起。观测员在岸上观测与其距离为S的浮标通过断面线所张的角度，称为视差。视差ρ″以角秒为单位，对于明视距离，通常取ρ″=60″。ρ″，S，ΔL三者的关系为

式中：206264.806是一个弧长相当的角秒数；距离S=D+x=Lbtgα+x，其中D为浮标起点距，Lb为基线长度，α为浮标的仪器视线与基线的夹角，x为观测员至断面起点桩的距离，通常较小，可忽略。

于是有

由此可知，起点距越大，ΔL越大，其最大值出现在对岸水边。取仪器视线照准对岸水边时，与基线夹角α=60°，tg60°=，得

另一方面，设观测员至水边距离为y，水面宽为B，可知S=B+y，y与河宽B相比可忽略，于是

从表面上看，瞄准误差引起的是断面间距误差，但在计算水面浮标通过上下断面的流速时，采用的距离不是浮标行程长度，而是断面间距，其值是固定的，所以实际上瞄准误差影响的是水面浮标的运行历时，使之产生误差Δt5，故有

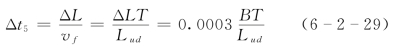
Δt5可正可负，为随机误差，假定服从正态分布且将其视为限差，则瞄准误差引起的运行历时误差标准差为

这是在上断面由于瞄准误差产生的运行历时误差标准差，对于上下两个断面，则有

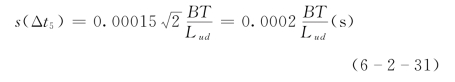
5.记时总误差

综上所述，记时误差来源及标准差列于表6-2-1。总记时误差标准差可通过各误差分量标准差合成求得。

表6-2-1　记时误差来源表

例6-2-1 某水文站上下断面间距Lud=200m，河宽B=500m，浮标运行历时T=100s，60s，求浮标运行历时误差标准差。

解：当运行历时T=100s，s（Δt1）=0.08s，s（Δt2）=0.17s，s（Δt3）=0.25s，s（Δt4）=0.29s，s（Δt5）=0.05s，运行历时总误差标准差为

相对标准差为

当运行历时T=60s，s（Δt1）=0.08s，s（Δt2）=0.10s，s（Δt3）=0.15s，s（Δt4）=0.029s，s（Δt5）=0.03s，运行历时总误差标准差为

相对标准差为

因此，浮标运行历时误差相对标准差可估计为0.5%。

（三）误差估计

如前所述，浮标上下断面间距误差标准差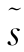（Lud）=0.1%，记时误差标准差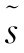（t）=0.5%，实测浮标流速误差标准差为

可见实测浮标流速误差主要来源于记时误差，断面间距误差可忽略不记。

现在考虑流速仪法施测水面流速的误差。设测站为一类精度站，高水，一点法，测速历时T=100s。由GB50179—93附表4-2查得Ⅰ型误差不确定度X′=7%，考虑到流速仪一点法取0.6相对水深的流速作为垂线平均流速，而多数情况下距水面越近，Ⅰ型误差越小，故取X′=6%，因该标准规定不确定度等于2倍标准差，所以Ⅰ型误差标准差s（ve）=3%，流速仪检定标准差s（vc）=0.5%，因只测水面流速故不计Ⅱ型误差，水面流速误差标准差可估计为

上述结果说明，实测浮标流速的测量精度高于流速仪水面一点流速的测量精度。在河段顺直且河段内各断面变化不大的情况下，河道水流为均匀流，各断面平均流速相等。显然，浮标流速是河段平均流速，问题是浮标流速代表的是浮标中断面的瞬时流速还是时均流速。如果代表的是瞬时流速，那么浮标流速应有较大的流速脉动误差；如果代表的是时均流速，那么也应有一定的流速脉动误差。总之，浮标流速存在流速脉动误差。在分析浮标流速误差源时，只考虑了断面间距和记时误差，实际上这两项误差相当于流速仪法的流速仪检定误差，而未计入与测速历时有关的流速脉动误差。

如将流速脉动误差计入浮标流速误差源，浮标运行历时即为测速历时，那么在上述算例中，实测浮标流速误差标准差为

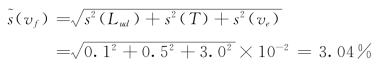
这样，浮标流速测量误差起码与流速仪法测速误差相当，而不至于小得太多。这个结果也说明，流速脉动误差是实测浮标流速的主要误差源。