水文测验误差分析：Ⅲ型误差标准差计算方法

（一）在已求得断面平均单宽流量误差方差情况下

如果按式（5-2-22）已求得断面平均单宽流量误差方差s2（Qu），可通过下述方法将部分单宽流量抽样误差方差分离出来。为此，将式（5-9-7）分别改写为

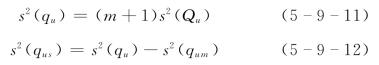
1.直接计算

根据测站测深和测速情况，确定部分单宽流量测量方差s2（qum）=s2（d）+s2（v），由式（5-9-12）直接求得部分单宽流量抽样误差方差s2（qus）。

2.经验公式

如同部分平均水深和部分平均流速抽样误差，部分单宽流量抽样误差也随部分宽的减小而减小，即随测速垂线数目的增多而减小。这是因为部分宽越小，垂线水深和垂线平均流速在部分宽内越接近直线分布，部分宽两端水深的算术平均值越接近部分平均水深的真值，部分宽两端垂线平均流速的算术平均值越接近部分平均流速的真值，从而部分单宽流量也越接近其真值。但部分单宽流量测量误差不随垂线数目的增多而减小。因此，可建立如下型式的经验公式

式中：s、t分别为待求参数。

经验公式建立方法与部分平均水深抽样误差方差经验公式相同。

求得各种垂线数目的部分单宽流量抽样误差方差后，按下式将其转换为断面平均单宽流量抽样误差标准差，亦即断面流量Ⅲ型误差标准差

（二）在已求得断面平均水深和断面平均流速抽样误差方差情况下

如果利用试验资料已求得断面平均水深和断面平均流速抽样误差方差，则可用式（5-9-10）将两者合成，得断面流量Ⅲ型误差方差。(www.xing528.com)

例5-9-1 利用兰西水文站1981年多线流量试验资料，计算断面流量Ⅲ型误差标准差。根据式（5-2-22）和式（5-2-23）计算的多线流量与少线流量相对误差方差和系统误差列于表5-9-1。

表5-9-1　兰西站多线流量与少线流量精简分析成果表

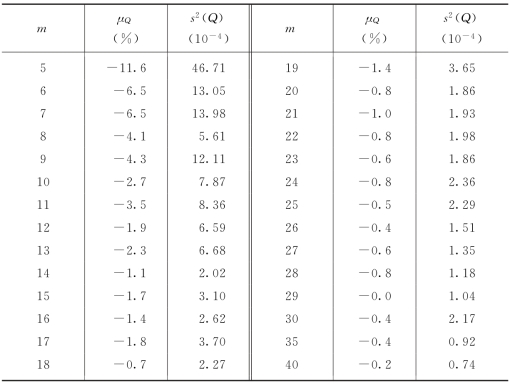
解：（1）常用方法。以s（Q）作为断面流量Ⅲ型误差标准差。以m=10为例，有

（2）推荐方法1。根据本站测深、测速情况，s2（qum）=17.0，m=10，有

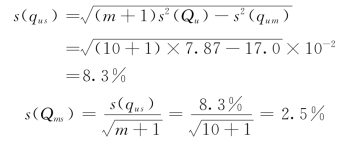
表5-9-2列出了s2（qum）分别为12.0、17.0、20.0时的经验公式参数和不同垂线数的s（Qms）值。

表5-9-2　断面流量Ⅲ型误差标准差计算结果比较表

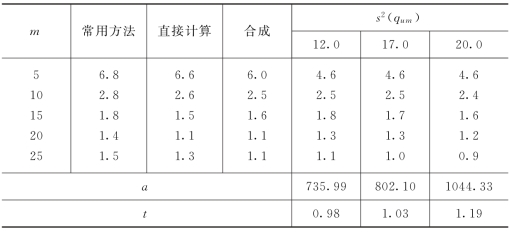
（3）推荐方法2。当m=10，第四章已求得s（d）=1.0%时的断面平均水深抽样误差标准差=1.6%，本章第五节求得s（v）=4.0%时的断面平均流速抽样误差标准差=1.9%，于是可将两者合成得

可见推荐方法1和推荐方法2的结果是一致的。

直接计算法简单易行，合成法适用于断面平均水深和断面平均流速抽样误差标准差已知，尤其适用于测深垂线和测速垂线数目不等的情况，经验公式可以求得任意垂线数Ⅲ型误差标准差，且可能便于综合。