指数x反映垂线平均流速总误差方差中其余误差随重复测量次数消减的速率,x越大,削减速率越快,反之亦然。在其他条件相同的情况下,x值越大,1-xJ越大,Ⅱ型误差方差越大。
由式(5-8-18)知,欲使1-xJ>0,应有kv>1/Jx,解得
![]()
kv<1,lnkv<0,所以x的下限应由各种计算规则计算出的折减系数kv的最小值决定。
在相关系数矩阵[rvjk]中,除对角线元素外,其余元素有大有小,有正有负,rv是其平均值,反映的是平均相关情况。rv大,kv大,1-xJ也大,Ⅱ型误差方差也大,这是因为rv越大,各次间的正相关部分增多,而Ⅱ型误差是由计算规则引起的,J次重复测量基本不变,Ⅱ型误差在总误差中占的比例增大了。
当相关系数矩阵[rvjk]中各元素均为1时,rv=1,kv=1,1-xJ=1,则有
![]()
说明垂线平均流速总误差中只有Ⅱ型误差,流速脉动误差等其余误差已不存在,只有这时才可以用式(5-8-1)计算Ⅱ型误差方差。因此,国家标准推荐的计算Ⅱ型误差方差公式,尽管避免了负值的出现,但一般而言,是不符合实际情况的。
当rv=0时,kv=1/J,必须取x=1,有1-xJ=0,从而
![]()
说明垂线平均流速总误差中已不存在Ⅱ型误差。但是,一般rv≠0,如果再取x=1,当rv<0时,就会出现s2(ve)<0的现象。
一般,当rv=(J-Jx)/Jx(J-1)时,kv=1/Jx,有1-xJ=0,所以1/Jx<kv<1,0<1-xJ<1,从而
![]()
例5-8-1 以黑龙江省双库站、兰西站、富拉尔基站的试验资料说明Ⅱ型误差计算方法[35]。
计算步骤如下:
(1)计算按各种计算规则计算的垂线平均流速与近似真值的相对误差,对于每种计算规则,构成I行J列误差矩阵。(https://www.xing528.com)
(2)计算误差矩阵中任意列的误差方差及其J次平均值s2(vt1)。
(3)计算各列(次)误差间相关系数及其平均值rv和折减系数kv。
(4)计算各行(垂线)误差的J次平均值δi,对I行求δi的方差s2(vtJ)。
(5)计算各行(垂线)误差方差及其I行平均值s2F。
(6)计算各行(垂线)误差间相关系数及其平均值rf。
(7)确定x值。设测站各种计算规则kv的最小值为kvmin,则x>-0.4343lnkvmin。例如,富拉尔基站kvmin=0.0555,x>-0.4343×(-2.8914)=1.26,取x=1.3;同理,双库站x=0.7,兰西站x=1.0。
(8)计算xJ,1-xJ,Ⅱ型误差方差s2(ve)。
双库站、兰西站、富拉尔基站3个站的计算结果分别见表5-8-1、表5-8-2和表5-8-3。由计算结果可以看出,x=1.0时的计算值与国际标准推荐公式计算结果相同。富拉尔基站五点法和三点法的rv均小于零,所以按国际标准推荐公式计算Ⅱ型误差方差出现小于零的不合理现象,其标准差成为虚数。
表5-8-1 双库站Ⅱ型误差计算成果表
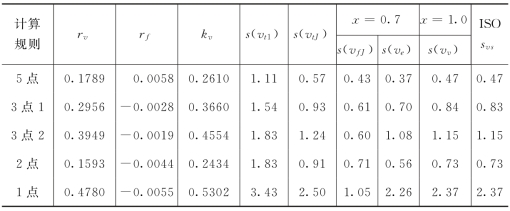
注 1.3点1是指普通三点法,3点2是指三点加权法,下同。
2.标准差的单位均为百分数,下同。
表5-8-2 兰西站Ⅱ型误差计算成果表
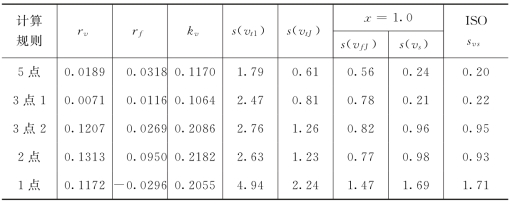
表5-8-3 富拉尔基站Ⅱ型误差计算成果表
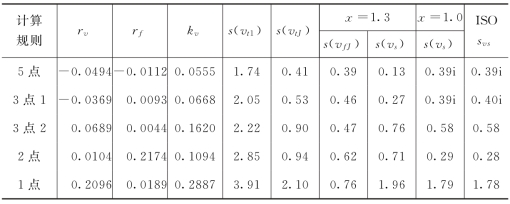
注 i为虚数单位,表明其平方为负数。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




