狄肯逊模型：误差分析与影响因素

（一）模型结构

狄肯逊模型是狄肯逊（W.T.Dickinson）于1967年研制的[20]，包括断面流量误差均值模型和方差模型。这里主要介绍方差模型。

断面流量采用中间部分法计算。误差方差为

式中：σvc为流速仪检定误差相对标准差；σvo为斜流引起的误差相对标准差；σvs为沿断面方向流速取样误差相对标准差；σvt为点流速时间抽样误差相对标准差；σvp为垂线流速分布剖面抽样误差相对标准差；σd为测深误差相对标准差；vji为测点时均流速，

其对应权重是Rji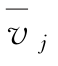；为第j条垂线的平均流速；fj为部分面积；m为断面上的垂线数；p为垂线上的测点数。

如果假定：①各误差分量的方差为常数；②点流速权重相等，Rji=1/p，由于

则有

（二）特点及评述

（1）在点流速误差中引进了斜流造成的误差分量，并认为该分量在点流速系统误差中占重要地位。在实际流量测验中，通常采用两种方法消除斜流产生的系统误差：一是当发现水流方向与测流断面不再垂直，且水流方向与断面法线方向的夹角达到某一限值时，可采用调整断面方向的办法消除斜流影响；二是流量测验中，测速同时测出流向偏角，然后修正点流速。(www.xing528.com)

（2）对垂线流速分布曲线抽样误差进行了较多理论分析。该项误差包括两个误差分量：一是选择的理论垂线流速分布曲线与测速点数及相应权重存在的误差；二是未能把流速仪放在正确位置带来的误差。

垂线流速分布的理论形式种类繁多。一旦选定某一种垂线流速分布，原则上垂线平均流速误差标准差与测点深误差标准差的关系就可以确定。但是，通常断面的垂线流速分布未知，只能假定为某一分布形式，然后对其平均误差和误差方差进行估算。这样求得的垂线流速分布抽样误差特征值带有很大任意性，缺乏用实测资料验证的依据。

（3）提出了测深误差由垂线水深沿断面方向的抽样误差、时间抽样误差和测量方法误差组成，即

式（5-4-11）中的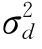即为以上三项误差分量方差和，并认为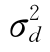与垂线数m成反比。

垂线水深沿断面方向的抽样误差实际是用水深代替部分平均水深所产生的代表性误差，这个观点具有理论意义和实用意义。但是，该模型没有给出推求这种抽样误差方差的方法。

（4）提出了流速误差中包括流速沿断面方向抽样误差分量，其方差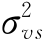与垂线数成反比。

流速沿断面方向抽样误差，实际是用垂线平均流速代替部分平均流速真值所产生的代表性误差。

（5）引进了部分流量不等权系数。实际上，本法的Cv（qj）与卡拉谢夫法的β是一致的。