卡特-安德森模型：水文测验误差分析30年研究

卡特-安德森模型是卡特（R.W.Cater）和安德森（I.E.Anderson）于1963年研发的[30，31]。他们不仅提出了断面流量随机误差计算模型，而且还根据大量试验资料给出了模型中各误差分量的计算方法和表列数据。在当时条件下，该模型不仅有重大的理论意义，还有较强的可操作性。应当说，卡特-安德森模型奠定了流量测验误差分析的基础。

（一）模型结构

该模型采用中间部分法计算断面流量。断面流量总误差方差为

式中：sRi为流速仪引起的断面流量相对误差标准差；sRt为流速脉动引起的断面流量相对误差标准差；sRs为垂线流速分布曲线引起的断面流量相对误差标准差；sRN为垂线数目的多少引起的断面流量相对误差标准差。

（二）误差分量的计算

1.流速脉动误差

设srt为点流速脉动误差标准差，它与断面流速脉动误差标准差的关系是

式中：Np为测点数。

为推求srt，在23条河流进行了流速脉动试验。在每条垂线的0.2、0.4、0.6、0.8相对水深处，测速1小时，每隔15秒记录一次。以测速历时为1小时计算的时间平均流速为点流速真值，计算各种测速历时的流速，并计算相对误差。然后，将不同河流、不同垂线同一相对水深及同一测速历时的相对误差合成为一个样本，计算标准差，即点流速脉动相对误差标准差srt。

2.垂线流速分布曲线引起的误差(www.xing528.com)

这项误差就是垂线上测点流速抽样误差，也可以说是计算规则引起的误差。在100条河流上进行了该项误差试验。每一条河流上布设25～30条垂线，每条垂线上布设11点测速。以11点计算的垂线平均流速作为近似真值，计算各种布点规则的垂线平均流速相对误差。将各条河流、各条垂线同一规则的相对误差合成一个样本，计算其标准差，即srs。

垂线流速取样误差引起的断面流量相对误差标准差按下式计算

式中：N为断面布设的垂线数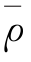；为垂线抽样误差间的平均相关系数。

3.垂线数目引起的误差

在127条河流上进行这项误差试验。在每个断面上布设100多条垂线，以所有垂线计算的断面流量作为近似真值，以总垂线数的1/2、1/4、1/5、1/7、1/10重新计算流量，计算各种垂线数目断面流量相对误差。将所有河流同一垂线数或接近的垂线数的相对误差作为一个样本，计算标准差，即sRN。试验结果表明，随着垂线数目的增加标准差减小。

（三）特点

（1）在断面流量随机误差计算中，首次提出三种抽样误差的概念。点流速脉动误差是点流速时间抽样误差，垂线流速分布曲线产生的误差是垂线上流速测点抽样误差，垂线数目引起的误差是垂线水深和垂线流速沿断面分布的抽样误差。这些概念至今仍是流量误差计算的基本概念。

（2）提出了将垂线上或部分断面上产生的误差标准差转化为断面相应误差标准差的方法。点流速脉动误差发生在测点上，用两点法计算的平均流速脉动误差发生在垂线上，利用式（5-4-2）就可以将其转换为断面流速脉动误差标准差。垂线流速分布曲线产生的误差发生在垂线上，利用式（5-4-3）可以将其转换为断面的相应误差标准差。

（3）利用大量试验资料分析各误差分量，具有实用价值。但该法没有考虑测深误差和测宽误差对断面流量误差的影响。