水文测验误差评定：断面平均水深抽样误差分析

在断面面积误差的三个分量中，水深测量误差和部分宽误差的计算方法前已叙及，这里关键的是断面平均水深抽样误差方差的确定。断面平均水深抽样误差也可称断面面积抽样误差，它是由断面上布设的测深垂线数目有限引起的，垂线数目越多，抽样误差越小，反之亦然。断面面积抽样误差标准差需利用多线断面测量资料来确定。

设有n次在不同水位下施测的多线断面资料，每次断面测量布设的垂线数目N均不少于50条。从多线断面中抽取m条垂线，m远小于N，计算少线断面的部分面积、断面平均水深和断面面积。少线断面布设的m条垂线将横断面分割成m+1部分，每一部分都含有若干条多线断面的测深垂线，用这些垂线计算的部分面积和部分平均水深分别作为该部分的面积和平均水深的近似真值。设第i次多线断面面积、平均水深分别为，相应的少线断面面积、平均水深分别为，由于少线断面与多线断面水面宽相同，故有

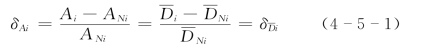
说明断面面积相对精简偏差等于断面平均水深相对精简偏差。根据精简分析及其误差的有关结论，应有

或

说明少线断面面积误差方差由精简偏差方差和多线断面面积误差方差两部分组成。多线断面垂线数目N越多，其误差标准差s（AN）越小，当垂线数目足够多时，s（AN）→0，此时有

同样有

上述论证说明，当多线断面的垂线数目足够多时，精简偏差方差等于少线断面面积误差方差，也等于少线断面平均水深误差方差。

因此，根据多线断面试验资料按下式计算的精简偏差方差和系统误差，即

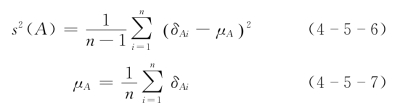
应等于少线断面面积总误差方差和系统误差，而且与下式的计算结果是等价的，即

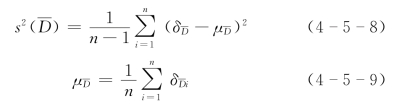
根据式（4-3-8）和按试验资料求得的，可得部分平均水深总误差方差为

如前所述，在部分平均水深总误差方差中，水深测量误差方差不随部分宽的宽度而变，亦即不随断面上布设的垂线数目而变，而抽样误差方差随部分宽的减小而减小，亦即随垂线数目的增多而减小。但是，对断面平均水深来说，其抽样误差方差和水深测量误差方差均随垂线数目的增多而减小。由于

只要知道s2（d），就可以求得。由于断面测量所用测深仪器、测具和测深方法是已知的，水深测量误差标准差可以比较准确估算，这样，就可以用下式直接计算各种垂线数目m的部分平均水深抽样误差方差，即(www.xing528.com)

试验资料分析表明，与m呈负指数关系，为此可建立如下形式的经验公式

式中：a，t为待定参数，可以通过回归分析求得。

有了部分平均水深抽样误差标准差，断面平均水深抽样误差标准差为

例4-5-1 黑龙江省兰西水文站曾于1981年进行多线流量试验。采用其断面测量资料来分析断面平均水深的抽样误差。多线断面测量的垂线数60～90，29个测次。根据式（4-5-8）和式（4-5-9）计算的断面平均水深总误差方差和系统误差列于表4-5-1。

解：按常规方法，表4-5-1中的μD即为断面平均水深抽样系统误差，为断面平均水深抽样误差方差。以m=10为例，。

表4-5-1　断面平均水深总误差计算结果表

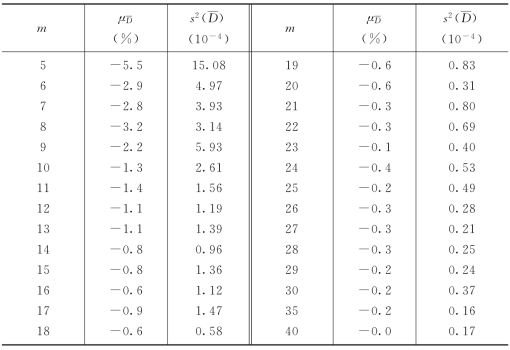
按本节论述，表4-5-1中的为断面平均水深总误差方差。为求抽样误差方差，需将水深测量误差方差分离。根据本站测深情况，选定水深测量误差标准差s（d）=1.0%，以m=10为例，有

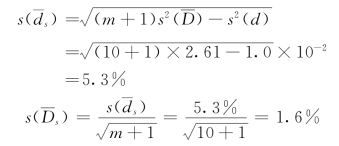
表4-5-2列出了取水深测量误差标准差s（d）=1.0%时，不同垂线数直接计算求得的断面平均水深抽样误差标准差。采用直接计算法简单易行。

还可以建立部分平均水深抽样误差方差与垂线数目的经验公式，其形式如式（4-5-13），对其两端取对数

令y=lns2，x=ln（m+1），b=lna，按第一章一元回归分析方法可得b，t，而a=eb。利用经验公式可求得任意垂线数的部分平均水深抽样误差标准差，然后将其转化为断面平均水深抽样误差标准差。

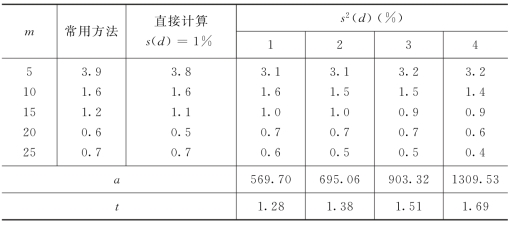
表4-5-2列出了s2（d）分别等于1%、2%、3%、4%时用经验公式计算的不同垂线数断面平均水深抽样误差标准差。回归方程相关系数均为0.68。由表4-5-2可知，取不同水深测量误差方差计算的断面平均水深抽样误差标准差差别不大，这是因为水深测量误差标准差本身不大的缘故。我们采用这种与常规方法差别不大的分析方法的目的，是为了揭示抽样误差的来源和本质，为断面流量抽样误差的计算奠定基础。

表4-5-2　断面平均水深抽样误差标准差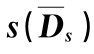计算结果比较表

回归方程相关系数均为0.68。由表4-5-2可知，取不同水深测量误差方差计算的断面平均水深抽样误差标准差差别不大，这是因为水深测量误差标准差本身不大的缘故。