水文测验误差分析与评定：标准差的计算方法

断面测量中，测深垂线通常等距布设，即部分水面宽相等，所以尽管实际工作中用部分水面宽加权法计算断面平均水深，实际上是用了算术平均法。因此，我们首先从式（4-3-2）入手，推求断面平均水深标准差。

对式（4-3-2）应用相对标准差传播律，得

式中：为断面平均水深相对标准差；为第j部分平均水深相对标准差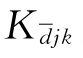；为第j和第k部分平均水深相对协方差。

因为部分平均水深总误差由抽样误差和测量误差组成，所以各部分平均水深相对误差可表示为

式中，括号的下标s表示该项误差是垂线平均水深的抽样误差，下标m表示该项误差是垂线平均水深的测量误差。考虑到抽样误差和测量误差独立，各垂线水深误差间独立，对以上各式进行求标准差运算，得

假定：①各部分平均水深抽样误差标准差相等，即；②各垂线水深测量误差标准差相等，即s（d1）=s（d2）=…=s（dm）=s（d）；③各垂线水深近似相等，即d1=d2=…=dm+1=d。于是可得

因为只有相邻部分的平均水深存在相同垂线水深，所以只计算相邻部分平均水深误差间的协方差，其余部分间的协方差均等于零。于是

于是有(www.xing528.com)

由式（4-3-5）和式（4-3-6）得

在各垂线水深相等的条件下，可得

令

则

式中：为断面平均水深抽样误差方差。

式（4-3-10）是从部分平均水深出发求得的断面平均水深误差标准差的计算公式，考虑了：①相邻部分平均水深误差协方差；②各部分平均水深误差标准差的不同；③部分平均水深和垂线水深误差标准差的区别。如果从式（4-3-2）出发但不考虑上述三项要求，同样可以推得式（4-3-8），这说明“考虑”的近似结果与“不考虑”的近似结果相同。如果从式（4-3-4）出发也可以推得类似于式（4-3-8）的公式，但不容易引进部分平均水深的抽样误差。