水文测验误差分析及评定：部分平均水深抽样误差

部分平均水深就是相邻垂线水深的算术平均值。取河道断面第j-1条垂线与第j条垂线间的第j部分来说明部分平均水深的误差组成。设在水位不变的某时段内对部分宽内的垂线水深进行了n次等精度测量。部分平均水深的真值为。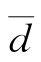

第j-1条垂线的水深：dj-1，1，dj-1，2，…，dj-1，n，近似真值为dj-1，0。

第j条垂线的水深：dj，1，dj，2，…，dj，n，近似真值为dj，0。

第j-1条和第j条垂线水深的算术平均值为

近似真值为

误差列为(www.xing528.com)

它是部分宽内首末两条垂线水深的算术平均值与部分平均水深真值的相对误差列。将该误差列变换为

该系列每一括号内的第一项是部分平均水深的估计值与算术平均值的真值的相对误差，这项误差是完全由测量引起的，称为部分平均水深测量误差；括号内的第二项是算术平均值的真值与部分平均水深真值的相对误差，这项误差不是由测量本身引起的，而是用首末两条垂线水深的算术平均值代替部分平均水深真值产生的代表性误差，称为部分平均水深抽样误差。上述分析表明，部分平均水深总误差由测量误差和抽样误差两部分组成。广义讲，抽样误差也应该属于测量误差，这里将其加以区分，不过是为了强调抽样误差的存在而已。

用式（4-1-2）计算断面面积，横断面被分割成m+1部分。在每一部分内，水深也会沿断面呈横向变化。若假定这种变化是单调的，那么根据积分中值定理，在部分宽内必有一点的水深等于部分平均水深。假若我们能够找到这一点，那么在这一点施测的水深恰好等于部分平均水深，水深测量也就不存在由于部分平均水深的代表性而产生的误差了。然而，由于天然河道横断面分布的复杂性以及时变性，部分平均水深的真值无法确切知道。无论用部分宽两端点水深的算术平均值，还是用部分宽中点的水深作为部分平均水深的估计值，都存在由于平均水深的代表性产生的误差。这种由于测深地点的选择所造成的部分平均水深的误差，也可称为水深横向抽样误差。

严格地讲，水深误差由时间抽样误差、横向抽样误差和测量误差三部分组成[20]。对于河床稳定或比较稳定的河流，水深时间抽样误差可以忽略不计。

直观上看，随着测深垂线数目的增多，部分水面宽减小，部分平均水深估计值对部分平均水深真值的代表性增大，水深横向抽样误差也随之减小，也就是说，水深横向抽样误差与测深垂线数目有关。而部分水深的测量误差则与垂线数目无关。