相关系数法与水文测验误差分析及评定书中证明的结果

同样，若假定各直接被测量的误差标准差相等，由式（3-3-3）得

相关系数矩阵R共有m2个元素，去掉主对角线上的元素1，还有m（m-1）个元素，这些相关系数的平均值为

于是

令

则有

由于s2（y）＞0，s2（x）＞0，应有kx＞0，于是

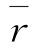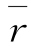解得＞-1/（m-1），是若干相关系数的平均值，应有≤1，因而有-1/（m-1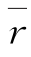）＜≤1，由此也可得0＜kx≤1。

上述论证说明，kx是个折减系数。式（3-3-18）表明函数的估计方差小于各直接被测量估计方差的平均值，函数使直接被测量的误差标准差坦化了，也可以说函数随机误差的分散性小于直接被测量随机误差的分散性。

若平均相关系数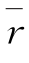=0，kx=1/m，则同样可得式（3-3-13）。这个结果说明，特征值法是相关系数法的一个特例。这是因为在推求相关系数矩阵特征值时，需将矩阵变换为对角矩阵，而对角矩阵除主对角线上的元素不为零外，其余元素均为零，这相当于相关系数法的平均相关系数等于零。

这里有一个细微的差别需要说明，若各直接被测量的误差互相独立，则必有平均相关系数等于零。而平均相关系数等于零，不见得各直接被测量的误差相互独立，因为任意两个直接被测量误差间的相关系数可能有正有负，一求和取平均，互相抵消了。

作为相关系数法的一个应用，以下来证明第二节的公式（3-2-8）。(www.xing528.com)

由第二节可知

由于

于是

式（3-3-21）右端大括号中：

所以

式（3-3-23）右端大括号内分别是：

将上述各项代入式（3-3-23），得

将s2r解出，便得

在流量测验Ⅱ型误差分析中将用到这个公式。