【摘要】：当被测量的估计值是由实验数据通过最小二乘法求得的回归方程得到时，可以求得回归方程、回归参数和估计值的标准不确定度。，n，利用最小二乘法求得回归直线=b0+b1x，给出X与Y之间的线性关系。对于多元线性回归和正交多项式回归，单个测量值标准不确定度、拟合参数标准不确定度和估计值的标准不确定度，也可以根据相应的实验标准差求得。若多元线性回归中有f个待求参数，则它们的自由度均为ν=n-f。
当被测量的估计值是由实验数据通过最小二乘法求得的回归方程得到时，可以求得回归方程、回归参数和估计值的标准不确定度。
由第一章可知，根据n对测量数据（xi，yi），i=1，2，…，n，利用最小二乘法求得回归直线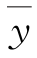
=b0+b1x，给出X与Y之间的线性关系。
单个测量值yi的实验标准差为
自由度ν=n-2。s（yi）反映了测量值yi对回归直线的分散性，s（yi）愈小，测量值yi与拟合直线的分散性愈小，拟合的可靠性愈高，它是直线拟合的质量标志。s（yi）也称为回归方程的实验标准差。
拟合参数b0，b1的实验标准差为
从拟合直线上查得估计值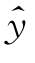
的实验标准差为(www.xing528.com)
于是，拟合直线的标准不确定度为
拟合参数的标准不确定度为
估计值的标准不确定度为
以上诸式中，
。u（yi）的自由度ν=n-2，根据自由度的性质（1），u（b0），u（b1）和
的自由度也应为n-2。
对于多元线性回归和正交多项式回归，单个测量值标准不确定度、拟合参数标准不确定度和估计值的标准不确定度，也可以根据相应的实验标准差求得。若多元线性回归中有f个待求参数，则它们的自由度均为ν=n-f。按照第一章的写法，回归方程中有m+1个待求参数，故它们的自由度均为ν=n-（m+1）。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
