测量误差传递的绝对公式

在重复测量中，由于单次测量的随机误差不能作为测量的质量指标，必须用表征测量系列分散性的标准差来评定其质量，同样函数的随机误差也必须用标准差来评定。因此，欲计算间接被测量的标准差，必须借助间接被测量与直接被测量的函数关系，建立间接被测量和直接被测量随机误差标准差之间的关系。这就是随机误差的传递问题。当间接被测量与直接被测量存在如式（1-7-1）的函数关系时，可以证明函数随机误差标准差为

式中：Kij为协方差，定义为

式中：ρij为第i个直接被测量和第j个直接被测量误差间的相关系数。

相关系数是衡量误差间是否存在线性关系的参数。相关系数的一个重要性质是其绝对值不大于1，即-1≤ρ≤1。当0＜ρ＜1时，两误差正相关，表现为一个误差增大时，另一个误差也增大；当-1＜ρ＜0时，两误差负相关，表现为一个误差增大时，另一个误差减小；当ρ=1时，两误差完全正相关；当ρ=-1时，两误差完全负相关。两误差完全相关，表明两者之间有确定的函数关系；当ρ=0时，两误差不存在相关关系，但不一定独立，而两误差独立必定不相关，只有当两误差服从正态分布时，不相关和独立才是等价的。

当ρ=0时，式（1-7-13）成为

这是实际工作中经常应用的公式。

式（1-7-13）是以绝对误差表示的随机误差传递公式。若以相对误差表示，则随机误差传递公式为

式中：为函数的相对标准差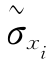；为第i个直接被测量的标准差，为第i个和第j个直接被测量的协方差，按下式计算

当ρ=0时，式（1-7-16）成为

现以几个简单函数形式为例，来说明用相对值表示的随机误差传递的计算过程，其中直接被测量间独立。

(1)y=x1±x2。

因为

所以

式（1-7-19）可以推广到多个直接被测量代数和的情况。

(2)y=x1x2。(www.xing528.com)

因为

θ1=θ2=1

所以

式（1-7-20）可以推广到多个直接被测量乘积的情况。

(3)y=。

因为

θ1=1,θ2=-1

所以

实际应用中，应注意以下几个问题：

1）σy与σx的一致性。若σx为单次测量的标准差，则σy也应为间接测量中单次求得值的标准差；若σx为算术平均值的标准差，则σy也应是算术平均值的标准差；若σx为极限误差，则σy也应是极限误差。对于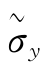和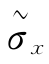也同样如此。

2）各直接被测量和间接被测量的标准差均为重复测量中按同一被测量计算的标准差，所以标准差的相对值就是相对误差的标准差。

3）实际测量中，应以实验标准差s（xi）代替误差传递公式中的σxi。同样，相关系数ρij也应用其估计值rij代替。rij按下式计算

式（1-7-13）、式（1-7-15）、式（1-7-16）、式（1-7-18）就是随机误差传递公式，或称随机误差传播公式，或称随机误差传播律。因为这些公式实际上是标准差传递公式，所以也称标准差传播律。