统计法判别异常值，水文测验误差评定

如果不能从物理上判别哪个测量值是异常值，则应采用统计法进行判别。

（一）3σ准则（拉依达准则）

设对某量进行等精度独立测量，形成测量系列xi，i=1，2，…，n，样本均值为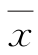，残差为υi=xi-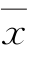，样本标准差为s。若测量列中的测量值只含有随机误差，则根据正态分布律，其残差落在±3σ以外的概率为0.3%，即在370次测量中只有1次其残差＞3σ。如果在测量过程中，发现有大于3σ的残差的测量值，则可认为该测量值含有粗大误差，应予以剔除。因σ2是总体方差，是未知的，而样本方差s2是σ2的估计值，所以在实际工作中用3s代替3σ。

3σ准则是最常用也是最简单的判别粗大误差的准则，它是以测量次数充分大为前提的，但通常测量次数较少，因此，3σ准则只是一个近似的准则。当测量次数在10次以下时，用3σ准则不能剔除任何数据，所以当测量次数在10次以下时，用这种方法不能剔除粗大误差[5]。

（二）t检验准则（罗曼诺夫斯基准则）

当测量次数较少时，可采用t检验准则，其特点是首先剔除一个可疑测量值，然后按t分布检验被剔除的测量值是否含有粗大误差。

不失一般性，假定xn为可疑数据，将其剔除后计算的平均值为（计算时不计xn）(www.xing528.com)

测量列标准差为（计算时不包括υn=xn-x）

根据测量次数n和选定的显著性水平α，按t分布检验系数K（n，α）来判别。若

则认为测量值xn含有粗大误差，剔除xn是正确的；否则，xn不含粗大误差，应予以保留。检验系数K（n，α）可查表[3，4]，也可以按下式计算[5]

此外，还有肖维勒准则、格拉布斯准则和狄克逊准则等，感兴趣的读者可查阅误差理论方面的专著[3，4，5]。

这些准则是针对同一被测量的重复测量提出的，原则上也适用于以相对误差表示的不同被测量的多次测量。