水位流量关系曲线中的t检验应用

（一）一个总体均值的假设检验

一个总体均值的假设检验包括总体方差已知和未知两种情况，这里主要介绍后者。

设总体服从正态分布N（μ，σ2），方差σ2未知，样本均值和方差分别为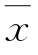和s2，现来检验总体均值。给出三种假设：

Ⅰ H0:μ=μ0 H1:μ≠μ0

Ⅱ H0:μ≥μ0 H1:μ＜μ0

Ⅲ H0:μ≤μ0 H1:μ＞μ0

其中μ0已知。假设H0称为零假设，假设H1称为备择假设。Ⅰ中的假设检验为双边假设检验，Ⅱ、Ⅲ中的假设检验为单边假设检验。

水文测验误差分析中，多数用到检验假设Ⅰ。对于Ⅰ，在假设H0为真的情况下，由第三节知，统计量

服从自由度ν=n-1的t分布。给定显著性水平α，查t分布表得临界值tα（n-1）[由于t分布表通常为双分位数表，故临界值写为tα（n-1）]。当使

即＞tα（n-1）为小概率事件，由样本值计算得t值，若≤tα（n-1），则接受原假设；否则，则拒绝原假设。

在水文测验工作中，当需要新仪器、新方法与传统仪器、传统方法进行比较，以及常用流速仪与备用流速仪进行比测时，通常用t检验对各对数据的偏离值进行检验，判别两者是否存在系统偏离，这就是成对出现的两组数据的比较问题[8]。

设两组数据的偏离值为di，i=1，2，…，n，其均值和标准差分别为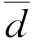和s。一般可认为偏差d服从正态分布。如果两组数据没有系统偏差，则偏差的总体期望值应为零，即μd=0。这样，问题变为检验假设H0：μd=0。在H0为真的情况下，统计量为

给定显著性水平α，当≤tα（n-1）时，则接受原假设，认为两组数据之间不存在显著系统偏差；否则，则拒绝原假设。

文献[8]针对两种测流方法、两种采样仪器的比较，以及自记水位计与人工观测水位的比较，列举了详尽算例。下面以两种测流方法的比较来说明具体算法。

例1-4-1 闽江文山里水文站将新的测流方法——多层积宽法与常规流速仪法进行了比测，部分比测资料见文献[8]。比测测点n=10，平均相对偏差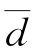=0.9%，标准差s=2.02%。试问两种方法所测结果有无系统偏离？(www.xing528.com)

解：采用t检验，检验假设

取显著性水平α=0.05，自由度ν=n-1=9，查t分布表得临界值tα（n-1）=2.26。由于t＜tα（n-1），故接受原假设，认为两种测流方法测得结果无显著偏离，即无显著系统误差。

（二）两个总体均值差异性检验

检验两个总体均值的差异性，与一个总体的假设检验相似。当两个总体方差σ21和σ22未知且相等时，需利用t检验来检验两个总体均值差异性。

设有X和Y两组测量系列：

x1,x2,…,xn1

y1,y2,…,yn2

其中n1和n2分别为X和Y样本的容量。令X和Y分别服从正态分布：N（μ1，σ2）和N（μ2，σ2），其中μ1为测量系列X总体均值，μ2为测量系列Y总体均值，σ2为共同的方差。设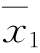 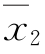， 分别为两个样本的均值，s1，s2分别为两个样本的标准差，可以证明统计量

服从自由度为n1+n2-2的t分布。令

则有

检验两个总体均值差异性可采用假设H0：μ1=μ2。在假设H0为真的条件下，μd=0，式（1-4-10）成为

给定显著性水平α，可查得临界值tα（n1+n2-2）。若＜tα（n1+n2-2），则接受原假设，认为两总体均值无显著差异，或两组测量数据来自同一总体；否则，则拒绝原假设。

如果不能确知两个总体方差相等，可通过随后介绍的F检验来检验。检验两个总体均值差异性的t检验在水位流量关系曲线的确定中得到应用。