《水文测验误差分析与评定》-随机误差的正态分布

正态分布是常见的一种概率分布。由于多数随机误差服从正态分布，因而正态分布在误差理论中占有重要地位。

如果连续型随机变量ξ的概率密度函数为

则称ξ服从正态分布，简记为ξ～N（μ，σ2），其中μ，σ2分别为总体期望值和方差。

由于随机误差具有抵偿性，对于有限次测量，随机误差的算术平均值是一个很小的值，当测量次数无限增多时，它趋于零。于是，随机误差服从的正态分布概率密度函数为

这是误差理论常用的正态分布形式，简记为N（0，σ2），其曲线形式见图1-2-1。

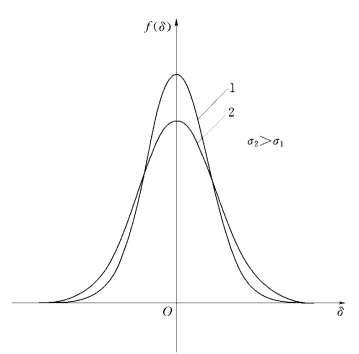
图1-2-1　正态分布密度曲线图

由图1-2-1可知，曲线呈对称分布，说明绝对值相等的正误差和负误差出现的机会相等，反映了随机误差的对称性。曲线在x=0处有一单峰，然后向两侧逐渐减小直至趋于零，反映了误差的单峰性和有界性。

随机误差不大于某一数值δ的概率为

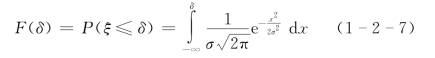
经变量代换，得

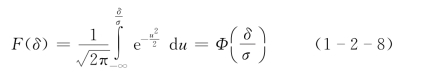
Φ（z）为标准正态变量的分布函数，对应的概率密度函数为

称为标准正态概率密度函数，简记为N（0，1）。Φ（z）的值见附表1。若已知σ，给定δ，由z=δ/σ查表得Φ（z）。利用式（1-2-8）可以求得服从正态分布的误差不大于某一数值的概率。

实际工作中经常遇到计算误差落在某一区间的概率。下面介绍几种形式略有差别但实质相同的计算方法。

（一）利用分布函数

由式（1-2-8）知

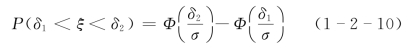
若δ2=δ，δ1=-δ，则

这是因为

（二）利用拉普拉斯函数

由式（1-2-8）知

式中(www.xing528.com)

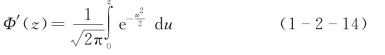
称为拉普拉斯函数，Φ′（z）也可制成表备查[4]。由于Φ′（-z）=-Φ′（z），故有

（三）利用误差函数

误差函数定义为

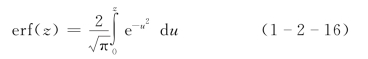
误差函数也可以制成表备查[4]。在式（1-2-13）中，若令v=，则

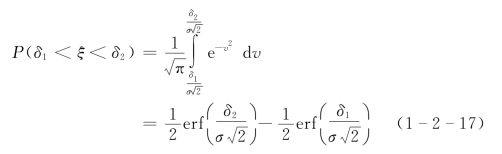
由于erf（-z）=-erf（z），故有

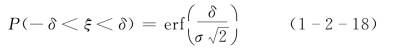
水文测验中经常用到的精简分析，要求分析测次不小于30次，将精测值与简测值对比，并规定：如果累积频率75%和95%的相对偏差分别不大于δ1和，那么精简分析符合要求，常测方案可使用。

因为参与分析的测次较多，可将累积频率近似地视为概率。于是

P(-δ1＜ξ＜δ2)=2Φ(z)-1=0.75

解得

Φ(z)=0.875

查表得

这意味着30个测次中大约有22次相对偏差须落在±1.15σ范围内。对于累积频率95%的相对偏差，同理可得

这意味着30个测次中大约有28次的相对偏差须落在±1.96σ范围内。

上述结果说明了75%、95%累积频率的相对偏差与相对标准差的关系。

例1-2-1 计算随机误差落在±σ，±2σ，±3σ范围内的概率。

解：由式（1-2-11）知

P(-σ＜ξ＜σ)=2Φ(1)-1=2×0.8413-1=0.6827

P(-2σ＜ξ＜2σ)=2Φ(2)-1=2×0.97725-1=0.9545

P(-3σ＜ξ＜3σ)=2Φ(3)-1=2×0.99865-1=0.9973

另一方面

由此可见，大约每3次测量中可能有1次的误差绝对值大于1倍标准差，每22次测量中可能有1次的误差绝对值大于2倍标准差，每370次测量中可能有1次的误差绝对值大于3倍标准差。测量次数一般很少超过几十次，可以认为误差绝对值大于3倍标准差几乎是不可能的，因而，有时将大于3倍标准差的误差作为粗大误差。