【摘要】：（一）单次测量标准差由于随机误差的存在，测量系列中各测得值一般不相同，它们围绕测量系列的算术平均值有一定分散性。，n，单次测量的标准差为式中：n为测量次数，应充分大。（二）平均值的标准差在相同条件下，对同一被测量作多组重复的系列测量，每一系列测量都有一个算术平均值，由于随机误差的存在，各系列的算术平均值并不相同，它们围绕着被测量的真值有一定分散程度。
（一）单次测量标准差
由于随机误差的存在，测量系列中各测得值一般不相同，它们围绕测量系列的算术平均值有一定分散性。单次测量的标准差就是表征测得值分散性的参数。标准差小，任意单次测得值对算术平均值的分散性就小，测量系列中小的误差占优势，测量的可靠性就大，测量的精度就高，所以也可以说单次测量标准差是衡量单次测量好坏的质量指标。
设有测量系列xi，被测量真值为x0，随机误差Δi=xix0，i=1，2，…，n，单次测量的标准差为
式中：n为测量次数，应充分大。一般情况下，真值未知，随机真误差也未知。所以，式（1-2-1）只是一个定义式，一般并不用它来计算标准差。
实际工作中，一般按下式来计算单次测量标准差，即样本标准差，也称实验标准偏差，或简称标准差，即
式中：xi为第i次测量结果；x为n次测量的算术平均值；υi为残差。
式（1-2-2）称为贝塞尔公式。(www.xing528.com)
s（xi）表示单次测量xi的标准差，并不表示函数关系，本书将用这种表示方法。
（二）平均值的标准差
在相同条件下，对同一被测量作多组重复的系列测量，每一系列测量都有一个算术平均值，由于随机误差的存在，各系列的算术平均值并不相同，它们围绕着被测量的真值有一定分散程度。平均值的标准差就是表征算术平均值分散性的参数。与式（1-2-1）对应的平均值的标准差为
而与式（1-2-2）对应的平均值实验标准差为
式中：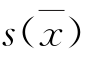
为平均值实验标准差，也称样本平均值标准差。
显然，测量次数越多，平均值越接近被测量的真值，测量的精度也越高，但当n＞20时，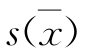
减少的速率变缓，而测量次数的增加意味着投入的增加，所以在水文测验中一般取n=20～30即可。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
