无量纲图表计算二阶效应

对于钢筋混凝土偏心受力构件，在计算正截面受压承载力时，应考虑结构侧移和构件挠曲引起的附加内力。在确定偏心受力构件内力设计值时，可近似考虑二阶弯矩对截面轴向压力偏心距的影响，参照《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG 3362—2018）第5.3.9条引入偏心距增大系数η：

将轴向压力对截面重心的偏心距乘以偏心距增大系数η，采用规范法将求解正截面受压承载力的有关计算公式中采用ηei代替为M/N+ea，由于该法计算考虑二阶效应的正截面承载力需要求解众多计算参数，因此有必要寻找便于应用的计算方法。

为了避免众多计算参数，而且使得考虑二阶效应的正截面承载力计算更具一般性，提出了一种考虑二阶效应的正截面承载力计算的无量纲图算法。值得注意的是，式（6.26）中附加偏心距ea=max {h/30，20 mm}，其值与截面高度有关，是不确定的。在计算考虑二阶效应的弯矩MⅡ时，存在：

式中：

其中：

从式6.27可看出，绘制无量纲图表可先不考虑附加偏心距ea的影响，只需在截面弯矩设计中叠加一项Nea即可。因此，若给定lc/h的值，就可以得到一组mⅡ-n的相关曲线，这里mⅡ为考虑二阶效应的名义弯矩，并且可得

将前述得到的mⅡ-n相关曲线绘制成图表可得考虑二阶效应的矩形截面对称配筋计算无量纲诺模图（图6.10—图6.17）：

图6.10　考虑二阶效应的矩形截面对称配筋计算诺模图（λ=25，HRB400）

(www.xing528.com)

图6.11　考虑二阶效应的矩形截面对称配筋计算诺模图（λ=40，HRB400）

图6.12　考虑二阶效应的矩形截面对称配筋计算诺模图（λ=50，HRB400）

图6.13　考虑二阶效应的矩形截面对称配筋计算诺模图（λ=60，HRB400）

图6.14　考虑二阶效应的矩形截面对称配筋计算诺模图（λ=70，HRB400）

图6.15　考虑二阶效应的矩形截面对称配筋计算诺模图（λ=80，HRB400）

图6.16　考虑二阶效应的矩形截面对称配筋计算诺模图（λ=90，HRB400）

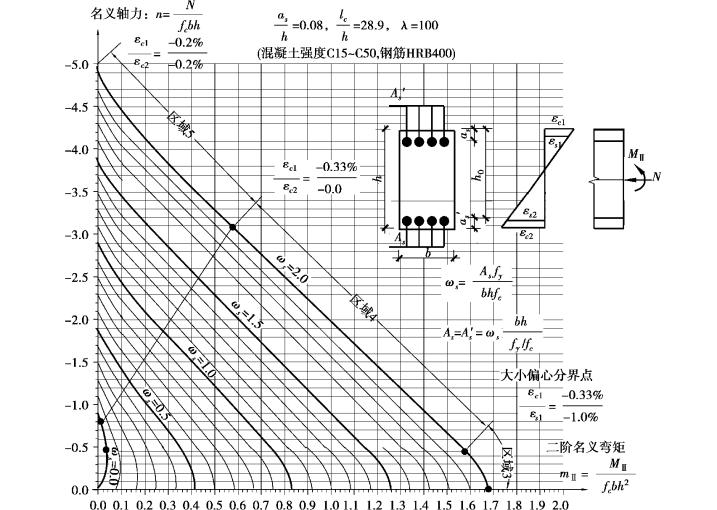
图6.17　考虑二阶效应的矩形截面对称配筋计算诺模图（λ=100，HRB400）

图6.10—图6.17考虑二阶效应的矩形截面对称配筋计算诺模图的使用说明：要求解考虑二阶效应钢筋混凝土矩形截面配筋需要从图中查得强度配筋率，首先需要根据第4章或第5章不同的结构形式选取不同的计算方法确定需要分析受压柱的计算长度，进而确定长细比λ，然后根据名义轴力n、二阶名义弯矩mⅡ及as/h，还有两个参数就是钢筋级别和混凝土的强度等级，经过简单换算就可得到考虑二阶效应钢筋混凝土矩形截面配筋量，这样就可以达到快速计算考虑二阶效应矩形截面受压柱配筋的目的，从而避免用规范法求解弯矩增大系数等众多参数求解，而且该方法能够很好地考虑同层柱之间的支援作用和层与层之间的支援作用，对于框架-剪力墙结构还能考虑剪力墙的侧向支援作用，有效弥补了规范法在考虑这些支援作用方面的不足。