二阶效应下钢筋混凝土截面弹塑性承载力的图解算法研究

在计算考虑二阶效应的钢筋混凝土偏心受压柱弹塑性承载力时，由《混凝土结构设计规范》第6.2.4条可以看出，通过弯矩增大系数考虑受压柱二阶效应时，柱计算长度作为其重要的参数，若按照规范计算长度系数法取框架柱的计算长度，将无法考虑同层柱之间的相互支援以及层与层之间的支援作用，当求解框架剪力墙结构的框架柱时还无法考虑剪力墙提供的侧向支撑作用，若基于第4章和第5章分别给出确定框架和框架-剪力墙结构的框架柱计算长度的计算方法，将能够很好地考虑这些支援的作用。截面承载能力也称为截面强度，对于钢筋混凝土短柱，截面承载力是其极限承载力，对于需要考虑二阶效应影响的钢筋混凝土细长柱，截面承载力是其极限承载力的上限值，因此，在分析稳定问题时，截面承载力计算是不可回避的问题。我国《混凝土结构设计规范》尽管给出了承载力计算的解析公式，但是应用公式求解前需要先判断截面的受力状态，再套用相应公式。规范给出了将截面的受力状态分为7种，分别是受弯（纯弯）、轴心受压、小偏心受压、大偏心受压、轴心受拉、小偏心受拉和大偏心受拉，如图6.1所示。一个截面的承载力对应了一组轴力-弯矩的数值，将其用图形表示就得到了图6.1所示的轴力-弯矩相关曲线，这个相关曲线也可以用来表示截面承载力[144]。

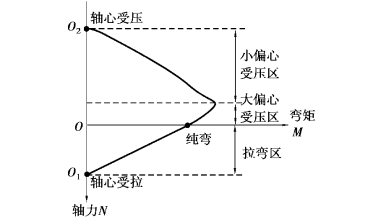
图6.1　截面的轴力-弯矩相关曲线

若要判别图6.1给出的截面受力状态类型较为不便，同时也给工程应用造成了不便。此外，在这些公式推导时采用了混凝土应力-应变关系的等效矩形应力换算，而等效矩形应力换算在理论上有两点不足之处：(www.xing528.com)

①换算时，只能用到《混凝土结构设计规范》中的σc-εc曲线的极限应变-3.3‰[图6.2（a）]，而不能运用整个本构曲线，这也意味着：无论作用大小，混凝土边缘应变始终为极限应变，这与实际受力不符，而实际受力是：作用小时，应变小，作用大时，应变大。

②压弯时（大偏压、小偏压）的极限应变是-3.3‰，轴心受压时的极限应变是-2.0‰，从压弯到轴压应变是跳跃变化，没有过渡，这也与实际受力不符。

本章采用由应变求解内力的方法，摒弃了等效矩形模型对钢筋和混凝土的应力-应变关系简化，通过分析极限承载力状态的应变变化区域，给出了钢筋混凝土矩形截面考虑二阶效应的轴力-弯矩相关曲线的诺模图，为考虑二阶效应的钢筋混凝土截面承载力的设计和配筋设计提供了一种简便的手算工具，并将钢筋混凝土截面承载力的计算结果与规范结果进行了对比验证。