图5.5所示框架-剪力墙结构在竖向荷载作用下发生侧移，剪力墙通过刚性楼板作用在框架层高处提供弹性支撑。由于框架-剪力墙结构通常应用于多层或高层建筑中，多层高层框架-剪力墙结构由于杆件众多，直接求解整体结构临界内外刚度比系数α是非常困难的。因此考虑将框架-剪力墙结构中的框架柱采用分离柱法[122]进行分离，单个分离柱的临界内外刚度比系数α在第2章中已经进行了推导，相当于将弹簧-摇摆柱模型中的弹簧用从框架-剪力墙结构中的分离柱来替换。确定结构单根分离柱临界内外刚度比系数后，再寻求单根分离柱与整体框架-剪力墙结构之间的关系，进而实现框架-剪力墙结构解析计算整体稳定的目标。
分离柱法将需要分析的局部柱从框架-剪力墙结构（图5.5）中分离出来，实现柱端约束等效，柱顶端和底端受到转动约束，其转动刚度分别为c1和c2，水平方向受到剪力墙提供的弹性约束，其侧移刚度为cw。框架-剪力墙结构的每根分离柱柱端约束都可以采用两个转动弹簧和一个水平弹簧进行模拟，如图5.6（a）所示。定义R1=c1/6ic，R2=c2/6ic，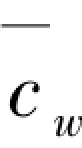
=cwh2/ic，ic为分离柱的线刚度，
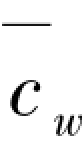为支撑弹簧相对刚度，由剪力墙提供。
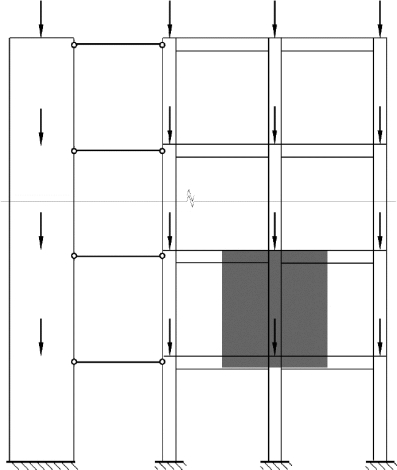
图5.5 框架-剪力墙结构简图
图5.6 分离柱计算简图
用三弹簧分离柱替换弹簧-摇摆柱模型中的弹簧，替换后的扩展结构如图5.6（b）所示。任意单根分离柱的临界方程与第2章推导的弹性侧移受压柱结构完全相同，则第i层（1≤i≤n）第j根（1≤j≤m）柱的临界状态方程可表示为：
式中 Nij———第i层第j根分离柱轴力；
αij———第i层第j根分离柱临界内外刚度比系数，可由第2章推导式（2.37）求得，即
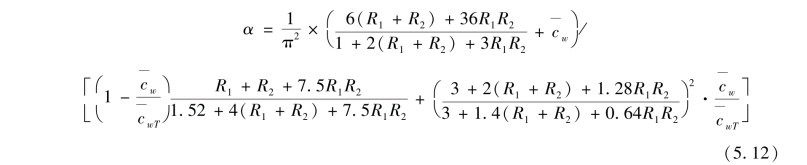
kij为任意分离柱的抗侧刚度，可由第2章推导式（2.32）求得，即(www.xing528.com)
式中 R1、R2———分别为柱上、下端横梁线刚度之和与柱线刚度之比。
当剪力墙提供的侧向支撑弹簧刚度cw≥cwT时，增大剪力墙刚度，无法进一步增加框架柱的临界承载力，因此取
=1，则各柱临界内外刚度比系数为：
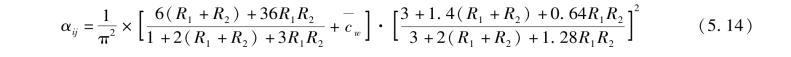
对于框架-剪力墙结构cwi≥cwTi所在楼层，可按该层楼层抗侧刚度平均分配于各柱，按照式（5.14）进行柱临界内外刚度比系数计算，工程中这种楼层一般都出现于建筑底部1～2层。层临界侧移刚度cwTi可按照式（5.15）进行计算：
式中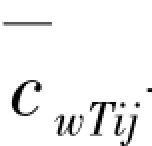 
———第i层第j根柱的临界侧移刚度，由式（2.33）或查表2.6计算；
EIcij———第i层第j根柱的抗弯刚度；
m———框架-剪力墙结构框架柱总根数。
当剪力墙提供给框架的侧向支撑弹簧刚度0＜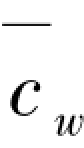
＜
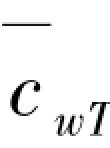时，经过计算发现，当R1和R2相差不大时（小于20倍），相对刚度
从零变化至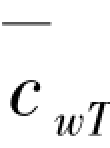
，式（5.12）计算所得α值变化均在4%以内，因此，可取
=0时对应的各柱临界内外刚度比系数进行近似计算：
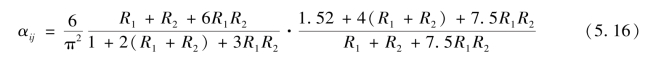
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
