弹簧-摇摆柱模型对框剪结构稳定性的解析计算方法研究

如图5.3（a）所示的单层框架-剪力墙（主结构），其结构稳定状态方程是超越方程，求解不便，特别是对杆件较多的框剪结构，直接求解就变得更加困难。摇摆柱自身是无法承载的，只有依附在主结构上，靠主结构提供刚度支持来进行承载，因此考虑采用摇摆柱建立框架-剪力墙的扩展结构，如图5.3（b）所示。扩展结构因框架和剪力墙上均无荷载，仅摇摆柱上作用荷载，其临界状态方程为代数方程，求解极方便。

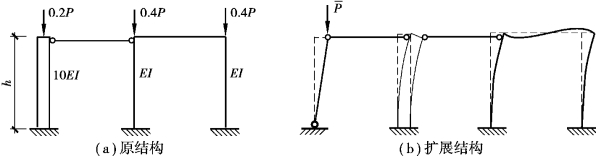
图5.3　单层框架-剪力墙

由于摇摆柱无法提供刚度，因此扩展结构与主结构具有相同的侧移刚度。扩展结构可简化为弹簧-摇摆柱模型，如图5.4所示。

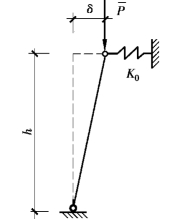
图5.4　弹簧-摇摆柱模型

如图5.4所示的弹簧-摇摆柱模型中弹簧刚度为K0，即主结构框架-剪力墙的抗侧刚度，在摇摆柱柱顶施加荷载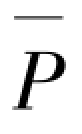，产生侧移δ，对下端取矩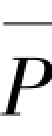：δ-K0δ·h=0，可得弹簧-摇摆柱结构临界状态表达式：(www.xing528.com)

式（5.8）物理意义为外荷载对弹簧刚度的削弱程度，当处于临界平衡状态时，弹簧刚度被削弱至零而失稳。外刚度KP随着外荷载P的增大而增大，当外荷载P=Pcr时，对应的外刚度Pcr/h称为临界外刚度，用KPcr表示。因此式（5.8）临界平衡方程可用框架-剪力墙结构的内外刚度进行表达：

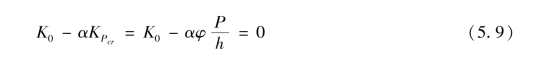
式中　α———临界内外刚度比系数，可以根据不同侧移类型按照第二章推导公式（2.15）、公式（2.26）和公式（2.37）计算；

φ———结构的整体临界因子，数值上φ=Pcr/P，根据该临界因子可根据式（5.10）判断框架-剪力墙结构的稳定性。

若假定图5.3（a）所示单层框架-剪力墙（主结构）的框架梁线刚度无穷大，则其内刚度K0=54EI/h3，即为结构的抗侧刚度，其扩展结构的临界力为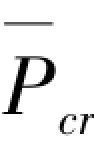=54EI/h2，主结构的临界力为：Pcr=4.5π2EI/h2。随着外荷载P增加，外刚度KP随之增加，当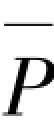→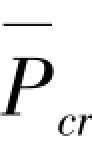时，主结构的抗侧刚度K0被削弱趋近于零，此时α=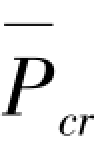/Pcr=1.216。从此例还可得出，当确定了框架-剪力墙结构的抗侧刚度（内刚度）K0和临界内外刚度比系数α后，很容易求解出主结构的临界承载力。