框架整体稳定性解析计算及结果比较

图4.14所示的四跨六层框架，在第四层处存在竖向收进以及抽柱，用本书方法求解结构临界承载力以及二层柱AB和三层柱CD计算长度系数。

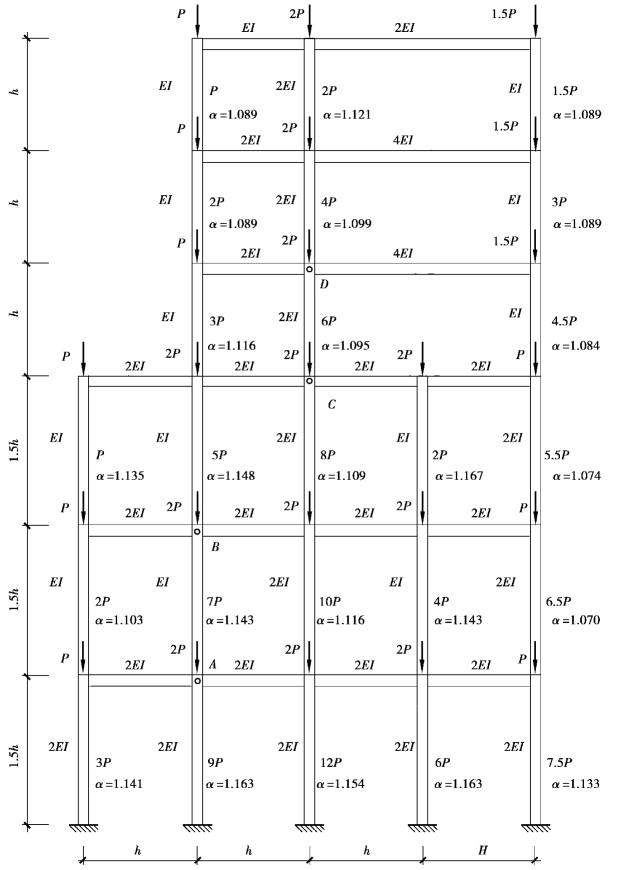
图4.14　四跨六层框架及轴力、二阶效应系数

（1）本书方法

按照算例3计算步骤进行计算，主要计算过程和计算结果列入表4.6。

表4.6　（Nmin）cr计算参数

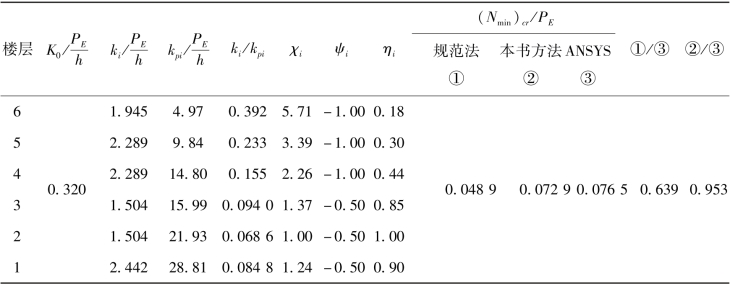
从表4.6可以看出，层最小内外刚度比系数所在楼层为第2层（薄弱层），其余各层存在富余刚度能够对薄弱层提供刚度支援，第6层层内外刚度比系数计算值为5.71，表明该层存在的富余刚度最大；第二层的相邻楼层第一层和第三层层支援系数相对其他楼层较大，表明这两个相邻楼层富余刚度提供的支援程度高，第6层层富余刚度最多，但其层支援系数仅为0.18，表明该层富余刚度对薄弱层的支援程度最低。本算例存在竖向收进及抽柱，属于较复杂的框架结构，从表4.6还可以看出，传统计算长度系数法求得（Nmin）cr值与有限元结果之比为0.639，偏差仍然很大，本章方法求得的（Nmin）cr值与有限元计算结果之比为0.953，吻合度较好且偏于安全，表明充分考虑了层与层的支援作用和同层柱之间的相互支援作用。

（2）规范法(www.xing528.com)

查《钢结构设计标准》附录E.0.2表，可求得各柱临界力Ncr和计算长度系数μ，计算结果列入表4.7。

表4.7　柱临界承载力及计算长度系数对比结果

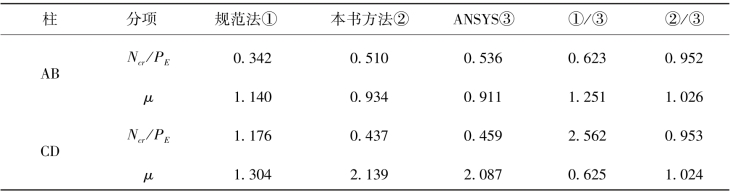
（3）有限元ANSYS求解

ANSYS求解时梁柱建模均采用简单的梁单元beam3，节点均为刚接，材料为弹性，即进行的计算是弹性屈曲分析（图4.15）。有限元ANSYS求得各柱临界力Ncr和计算长度系数μ，计算结果列入表4.7。

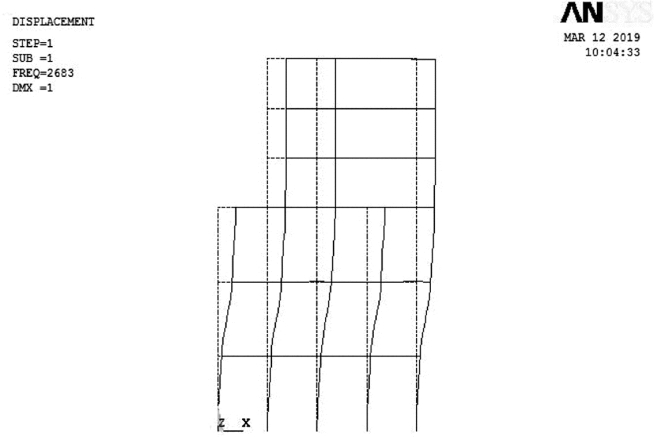
图4.15　三跨六层抽柱框架屈曲模态图

将本书方法、规范法和有限元ANSYS的计算结果归纳在表4.7，以便对3种方法的计算结果进行比较。

从表4.7结果可见，柱AB和柱CD采用计算长度系数法求得的计算长度系数与ANSYS计算结果相比误差仍然很大，AB柱计算长度比ANSYS大了25%，临界力小了38%，低估了该柱临界承载力，偏于保守；CD柱计算长度比ANSYS小了37%，临界力大了156%，同样严重高估了该柱临界承载力，存在极大的安全隐患。本书计算的柱计算长度系数与有限元计算结果比值分别为1.026、1.024，吻合度好。由此可看出，本书计算方法同样适用于复杂的框架结构临界承载力计算，且具有一定的精度。