假定楼层重复单元合适的边界条件[图4.4(a)],忽略杆件轴力影响;假定反弯点在柱中和梁跨中,则框架结构楼层重复单元的梁柱变形,如图4.4(b)所示,有如下关系:

式(4.5)中,γ为剪切角,也可称为弦切角,即框架柱变形后弦线与铅垂线之间的夹角。从式(4.4)和式(4.5)可得出层抗侧刚度k=(GA)/h,对于单跨框架重复单元[图4.4(a)],容易求出层抗侧刚度
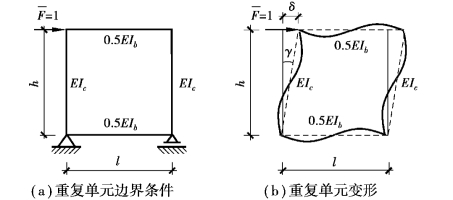
图4.4 楼层重复单元计算简图
多跨框架其重复单元(图4.5)由于仍属于高次超静定问题,直接求其层抗侧刚度的精确解是较为困难,为此可作适当简化,即假定边柱剪力是中柱剪力的1/2,其依据来自多跨框架楼层重复单元边柱与中柱相比柱端约束弱,两者的抗侧刚度D值比值大约为1/2。因此,可假定边柱剪力是中柱的1/2,这样就容易求解出层抗侧刚度,使得问题大为简化。同样在多跨框架楼层重复结构单元顶部施加单位力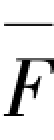 ,其1/2对称楼层重复单元的弯矩图如图4.6所示(图中m为楼层重复单元的柱总根数)。
,其1/2对称楼层重复单元的弯矩图如图4.6所示(图中m为楼层重复单元的柱总根数)。
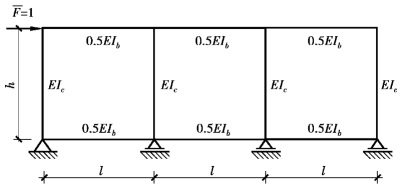
图4.5 多跨框架楼层重复单元
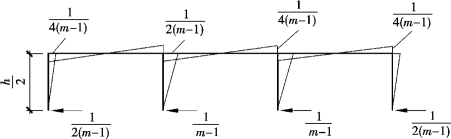
图4.6 1/2对称楼层重复单元弯矩图(https://www.xing528.com)
用图乘法可以求得单位水平力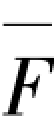 作用点处的水平位移δ。
作用点处的水平位移δ。

根据框架变形几何关系[图4.4(b)],可求得:
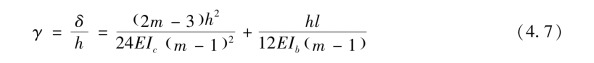
根据式(4.4)、式(4.5)及式(4.7)可求得框架层抗侧刚度,也称为框架层内刚度:
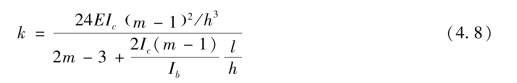
框架底层受固端约束影响反弯点常常不在柱中,受此影响若采用式(4.8)计算底层内刚度存在一定偏差,因此对框架底层采用反弯点在层高2/3的假定[75]。由于固端约束可视为刚度无穷大的梁,因此利用楼层重复单元计算层抗侧刚度时将底层梁惯性矩乘2m+1的放大系数加以修正,按照前述图乘法计算得到底层层抗侧刚度近似计算公式为:
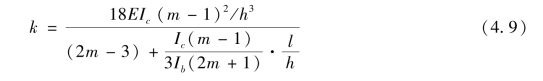
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




