框架结构的二阶内外刚度分析

从图4.1结构二阶内外弯矩关系图可以看出：各条二阶荷载弯矩线斜率为数值上等于作用于压杆的轴向力Pi，即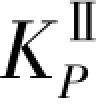=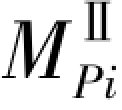/y=Pi，称其为二阶外刚度，仅与外荷载有关，用KⅡP表示。临界状态弯矩线斜率对应值：MⅡi/y=（π2EI）/l2与外荷载无关，称为二阶内刚度（固有刚度），用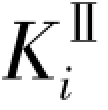表示。结构的平衡稳定状态关系式（4.1）可以采用二阶内、外刚度表示：

当框架失稳时，结构二阶内刚度被外荷载引起的二阶外刚度消耗为零。从量纲上看二阶内、外刚度属于力的量纲，一阶内外刚度的量纲为力/长度的量纲，从量纲统一的角度可以看出二阶内外刚度与一阶内外刚度之间的关系式为：

对于如图4.1所示的两端铰接的受压杆，其二阶荷载外刚度为KⅡP=P，则一阶荷载外刚度；二阶内刚度为，则一阶内刚度，即为杆件的抗侧刚度，也由此可以验证公式（4.3）的正确性。(www.xing528.com)

当框架失稳时，相当于框架的抗侧刚度（内刚度）被荷载外刚度消耗为零。框架结构临界承载力可将弹簧-摇摆柱模型中的弹簧采用框架替代，建立主结构框架的扩展结构，寻找两者之间的关系，进而求得框架结构的临界承载力，以单层框架为例，如图4.2所示。

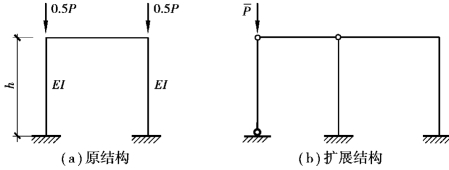
图4.2　单层框架

若假定图4.2（a）单层框架（主结构）的框架梁线刚度无穷大，则其内刚度K0=（24EI）/h3，即为框架的抗侧刚度，其扩展结构的临界力为=（24EI）/h2，原结构的临界力为：Pcr=（2π2EI）/h2。随着外荷载P增加，外刚度KP随之增加，当→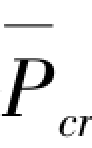时，主结构的抗侧刚度K0被削弱趋近于零，此时α=/Pcr=1.216，即此时有侧移框架柱临界内外刚度比系数为1.216。从此例还可得出，当确定了框架结构的抗侧刚度（内刚度）K0和有侧移框架柱的临界内外刚度比系数α后，很容易求解出框架结构（主结构）的临界承载力。