应用算例与验证：研究框架和框剪结构整体稳定性的解析计算方法

前面推导的计算长度系数公式不仅能考虑框架左右节点荷载不同带来的同层柱相互支援作用，而且还能考虑框架上下节点荷载不同带来的上下柱相互支援作用。若用《钢结构设计标准》附录E的表格来确定计算长度系数是不能考虑这些特性的，因为会导致不安全及过于保守的情况出现。为了展示这种差别，下面就单层、双层、三层单跨和三层多跨框架各选取一个算例，用本书方法和规范法进行计算和比较，同时也用有限元ANSYS进行计算，以便对两种方法的计算结果进行比较。

例题1：挠度法求解带摇摆柱单层框架

一单层框架带一跨摇摆柱为例，框架的几何参数及节点荷载如图3.12所示。

（1）本书方法

将已知荷载代入式（3.13）可求得：

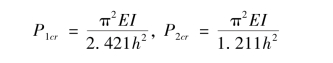
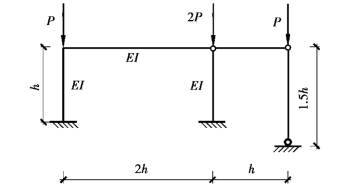
图3.12　带摇摆柱的单层框架

由式（3.14）可以求得：

（2）规范法

查附录E.0.2表，可求得μ1=μ2=1.300。

（3）有限元ANSYS求解

ANSYS求解时梁柱建模均采用简单的梁单元beam3，节点均为刚接，材料为弹性，即进行的计算是弹性屈曲分析（图3.13）。有限元ANSYS求得的精确解为μ1=1.548，μ2=1.095。

通过上述3种方法计算对比可以看出，规范法由于无法考虑左右柱之间的相互支援，左柱的计算长度比ANSYS小了20%，临界力大了42%，高估了左柱临界力，偏于不安全。挠度法计算结果与精确解误差在1%以内，计算精度很高。

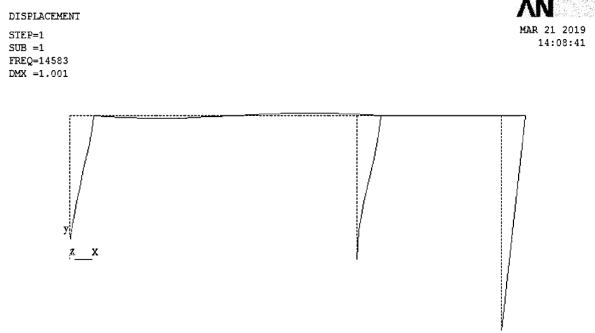
图3.13　单层框架屈曲模态图

例题2：挠度法求解双层框架

以图3.14所示的双层框架为例，各节点的荷载均不相同。

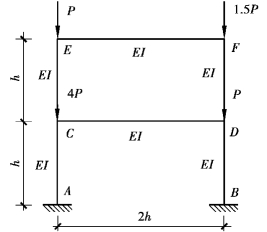
图3.14　双层框架

（1）本书方法

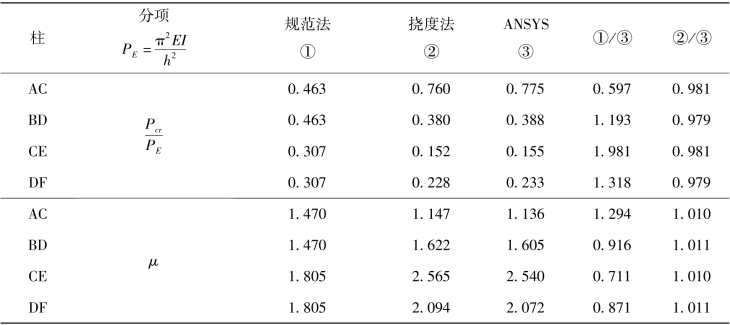
将已知荷载代入式（3.16）求得各柱临界力Ncr，并由式（3.17）可求出各柱的计算长度系数，计算结果列入表3.5。

表3.5　柱稳定承载力及计算长度系数对比结果

（2）规范法

查钢结构规范附录E.0.2表，可求得各柱临界力Ncr和计算长度系数μ，计算结果列入表3.5。

（3）有限元ANSYS求解

ANSYS求解时梁柱建模均采用简单的梁单元beam3，节点均为刚接，材料为弹性，即进行的计算是弹性屈曲分析（图3.15）。有限元ANSYS求得各柱临界力Ncr和计算长度系数μ，计算结果列入表3.5。

将本书方法、规范法和有限元ANSYS的计算结果归纳在表3.5，以便对3种方法的计算结果进行比较（图3.17）。

图3.15　双层框架屈曲模态图

从表3.5可以看出，挠度法计算结果与ANSYS对比误差很小，均在2%以内，表明充分考虑了同层柱支援和层与层之间的支援作用。规范法计算结果与ANSYS对比偏差很大，如CE柱临界力是ANSYS的1.981倍，严重高估该柱的临界力，极为不安全。

例题3：挠度法求解三层框架

图3.16所示为三层框架，各节点荷载可均不相同。

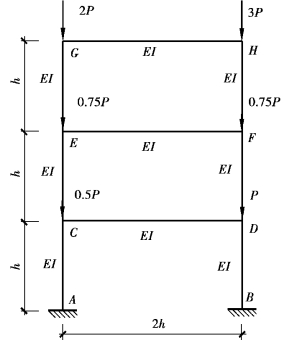
图3.16　三层框架(www.xing528.com)

（1）本书方法

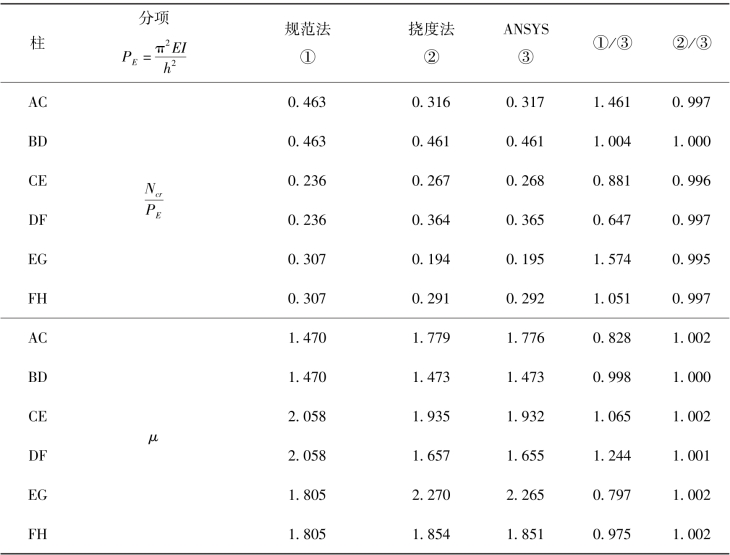
将已知荷载代入式（3.18）求得各柱临界力Ncr，并由式（3.17）可求出各柱的计算长度系数μij，计算结果列入表3.6。

（2）规范法

查《钢结构设计标准》附录E.0.2表，可求得各柱临界力Ncr和计算长度系数μij，计算结果列入表3.6。

表3.6　柱稳定承载力及计算长度系数对比结果

（3）有限元ANSYS求解

有限元ANSYS求得临界力Ncr和计算长度系数μij，计算结果列入表3.6。

将本书方法、规范法和有限元ANSYS的计算结果归纳在表3.6，以便对3种方法的计算结果进行比较（图3.17）。

从表3.6结果可见，挠度法计算结果与ANSYS对比误差同样很小，均在1%以内。而规范法计算结果偏差仍是很大，如EG柱临界力是ANSYS计算的1.574倍，同样高估了EG柱的临界力，是极为不安全的。

图3.17　单跨三层框架屈曲模态图

例题4：挠度法求解多层多跨框架

如图3.18所示的三层两跨框架，各节点荷载及框架参数如图3.18所示，多跨框架也按照本书挠度法进行求解。

（1）挠度法求解两跨多层框架临界力

①根据框架屈曲变形特点，选取表中近似变形形状，绘制在竖向荷载作用下的弯矩图，如图3.18（b）所示。

②根据表3.2查取标准反弯点，并按照表3.3和表3.4进行反弯点修正，综合考虑式（3.9），求解绘制各层处单位水平力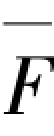=1作用下弯矩图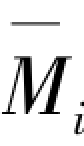，如图3.19所示。弯矩图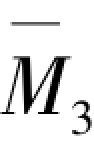为单位水平力作用在底层层顶时框架弯矩图与其他两层单位荷载作用弯矩图，确定方法相同，在此不再列出。

③根据杆件变形特点，按照表3.1选择合理的图乘系数，由式（3.5）对竖向荷载作用下弯矩图M与各层处单位水平力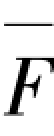=1作用下弯矩图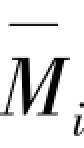分别进行图乘，列出n个关于侧移δi方程组，并使得关于侧移δi方程组的系数行列式为零进行求解，计算得出框架稳定承载力Pcr。按照表3.1选择合理的弯矩图乘系数，由式（3.5）对竖向荷载作用下弯矩图M[图3.18（b）]与各层处单位水平力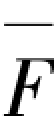=1作用下弯矩图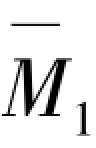、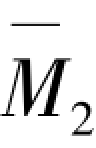和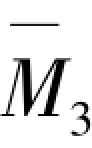（图3.19）分别进行图乘，可得：

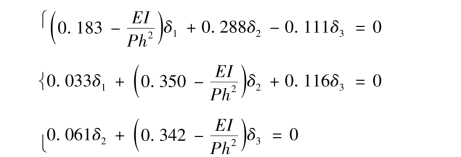
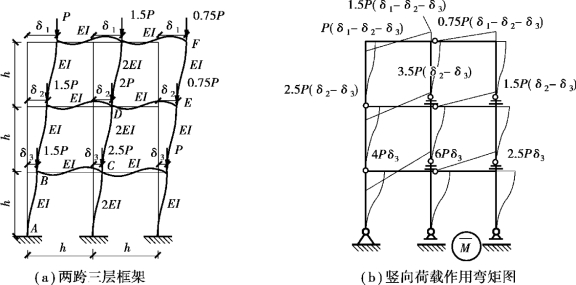
图3.18　两跨三层框架及弯矩图

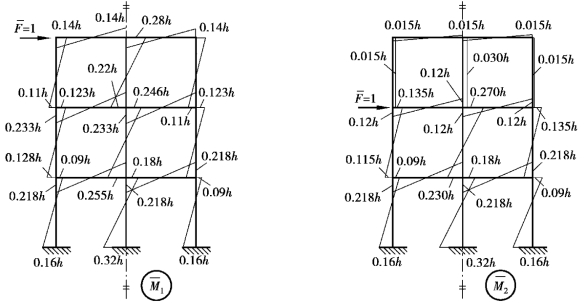
图3.19　单位水平荷载作用下弯矩图，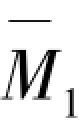

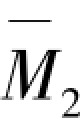
若要使得上述方程组成立，则需要上述方程组系数行列式为零，可以得到方程

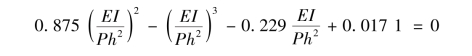
求解可以得到（EI）/（Ph2）最大正数解为0.452，据此可求出：Pcr=（π2EI）/（4.461h2），根据式[3.16（a）]和式（3.17）求得各柱承载力与计算长度系数，见表3.7。

（2）规范法

查《钢结构设计标准》附录E.0.2表，可求得各柱临界力Ncr和计算长度系数μ，计算结果列入表3.7。

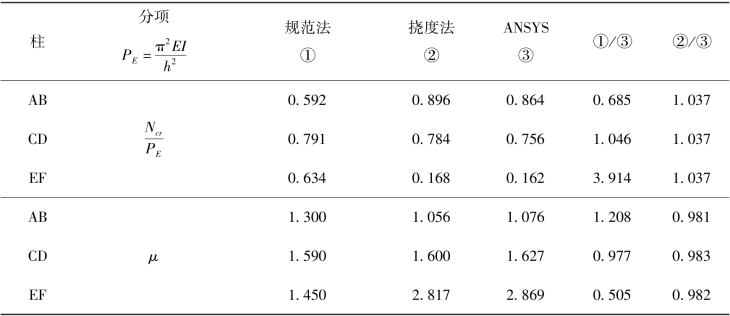
表3.7　柱稳定承载力及计算长度系数对比结果

（3）有限元ANSYS求解

ANSYS求解时梁柱建模均采用简单的梁单元beam3，节点均为刚接，材料为弹性，即进行的计算是弹性屈曲分析（图3.20）。有限元ANSYS求得各柱临界力Ncr和计算长度系数μ，计算结果列入表3.7。

图3.20　双跨三层框架屈曲模态图

将本书方法、规范法和有限元ANSYS的计算结果归纳在表3.6，以便对3种方法的计算结果进行比较。

由表3.7结果可见，规范提供的计算长度系数法求得临界力Ncr值与有限元结果之比为0.685，偏差很大。挠度法求得的Ncr值与有限元计算结果之比为1.037，吻合度较好且偏于安全。从表3.7结果可见，柱AB、柱CD和柱EF采用计算长度系数法求得的计算长度系数与有限元计算结果比值分别为1.208、0.977和0.505，误差较大，特别是柱EF临界力比ANSYS大了2.914倍，计算长度系数小了50%，严重高估该柱的临界力，偏于不安全。本书挠度法计算的柱计算长度系数与有限元计算结果比值分别为0.981、0.983和0.982，吻合度较好，表明充分考虑了同层柱支援与层与层之间的支援作用。