单层框架挠度法计算研究

为了更一般化，选取图3.7所示的带摇摆柱的单层框架为研究对象，框架左右柱的荷载不同，即P1=ξ1P、P2=ξ2P，Nj=χjP、Nn=χnP，框架失稳时柱顶产生侧移δ，柱子两端有转动约束，失稳曲线应呈双曲形状，故选取柱子的失稳定曲线为如图3.7所示。

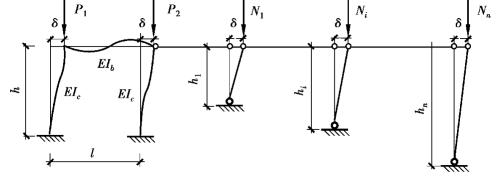
图3.7　带摇摆柱的单层框架

倾斜的摇摆柱将对其柱脚产生一倾覆力矩，这一倾覆力矩相当于对框架施加了一假想水平力T：

式中　m———摇摆柱的总根数；

Nj———任意第j根摇摆柱柱顶集中力；

hj———任意第j根摇摆柱高；

χj———任意第j根摇摆柱荷载比例系数；

P———各柱顶集中荷载的公因子，即存在Nj=χjP。

在求超静定框架柱顶侧移时，可选取超静定框架的基本体系（静定框架）计算荷载弯矩M，在原超静定框架上计算单位荷载弯矩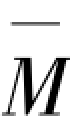。柱子的荷载弯矩是轴力在假设的失稳变形曲线上引起的，是二阶弯矩，其值为轴力与变形的乘积[图3.8（a）]；同样容易计算得到假想水平力作用下静定弯矩[图3.8（b）]；单位力作用在原框架上，其引起的弯矩为超静定弯矩，可由式（3.8）所求得反弯点得到单位荷载弯矩图[图3.8（c）]。

将图3.8（a）与图3.8（b）中的弯矩分别与图3.8（c）中单位荷载弯矩图乘，在表3.1可查

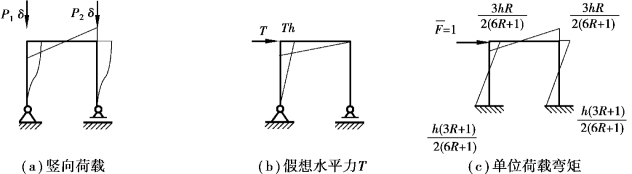
图3.8　单层框架计算简图

得相应的图乘系数，其图乘结果见式（3.12）：

(www.xing528.com)

等式两边消掉δ，可得：

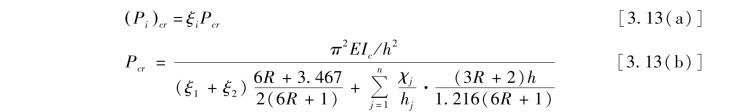
式中　E———弹性模量；

Ib———框架梁截面惯性矩；

Ic———框架柱截面惯性矩；

h———框架柱高；

P1cr，P2cr———框架左柱、右柱的临界荷载；

ξ1，ξ2———框架左柱、右柱的荷载比例系数，即柱顶作用荷载存在P1=ξ1P和P2=ξ2P；

Pcr———临界荷载因子；

R———梁柱线刚度比，等于ib/ic。

由式（3.13）可求得各柱计算长度系数：

式中　i，j———框架柱根数和摇摆柱的根数；i=1，2；j=1，2，…，n

R———梁柱线刚度比等于ib/ic。

该项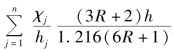为摇摆柱对临界力的影响项，无摇摆柱作用时该项为零，即为单层框架。