研究框架及框剪结构整体稳定性解析计算方法

取各层层高相同、各层梁柱线刚度相等的框架来分析，假定横梁的反弯点在跨度中央，且该点无竖向位移，据此，对于多跨多层框架的边柱，可用图3.4（a）表示，对于中柱来说，梁线刚度ib为左右两梁的线刚度之和。

为求解单柱的反弯点，选取每层柱的下端弯矩作为超静定结构的未知量，如图3.4（a）所示。对每层柱的下端可写出一个变形连续条件方程[75]：

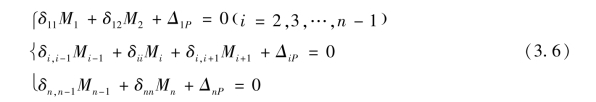
式中　n———框架的总层数；

Mi———任意第i层柱的下端弯矩；

δii———任意第i层柱的主柔度系数；

δi，i-1和δi，i+1———任意第i层柱的副柔度系数；

Δ1P、ΔiP和ΔnP———分别为底层、任意第i层和第n层的荷载作用自由项。

图3.4　单柱多层框架

为求解式（3.6）中的各柔度系数δij和ΔiP（i，j=1，2，3，…，n），将图3.4（b）中的任意第i层的弯矩Mi=1作用在静定基本体系上所产生的弯矩图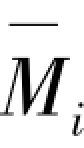与顶部单位水平力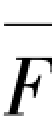作用在静定基本结构上所产生的弯矩图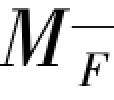进行图乘，可求出各柔度系数。再由式（3.6）可求得到各层柱下端弯矩Mi进而可用式（3.7）确定各层柱的反弯点高度比ηi：(www.xing528.com)

计算式（3.6）中的柔度系数因为需要求解方程组较为耗时和不便，作者经过推导得到式（3.8），用该式计算反弯点高度比ηi更方便，只需计算梁柱线刚度比R=ib/ic。

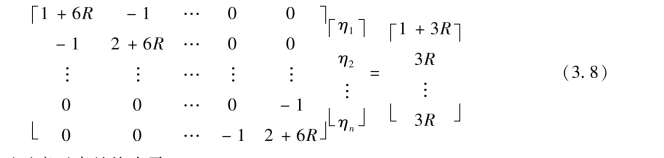
式中，系数矩阵无示意元素处均为零。

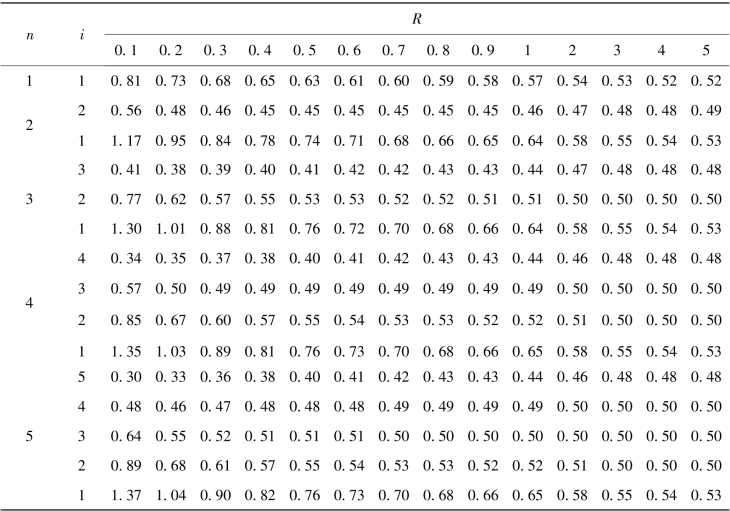
根据式（3.8）求出各层柱反弯点高度比η后，便可容易得出在顶部单位水平荷载作用下的框架弯矩图。为便于单位水平荷载作用下的框架弯矩图绘制，将式（3.8）所求得各层柱反弯点高度比制成表格（表3.2）。

表3.2　标准框架柱反弯点高度比η0

当单位水平荷载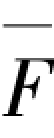施加在中间i层楼层处（非框架顶层）时，应按总层数为i的框架计算各柱反弯点，并绘制框架弯矩图，对于相邻的第i+1层柱弯矩可按经函数拟合所得式（3.9）近似计算，第i+2层柱弯矩及其以上各层弯矩均取为零。

式中　Mi+1———第i+1层柱弯矩，沿该层柱全高不变，弯矩方向与第i层柱顶弯矩方向相反；

Mi顶———第i层柱顶弯矩，可由式（3.9）计算得到。