确定挠度法弯矩图的图乘系数-解析计算方法研究

求解简支梁跨中挠度的式（3.2）—式（3.4）可以统一写为：

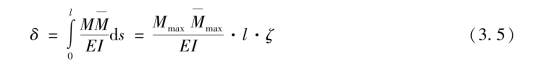
式中　Mmax———杆件屈曲时的最大弯矩；

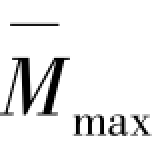———单位荷载作用下的最大弯矩；

ζ———图乘系数。

为便于挠度法图乘计算，选取常用的柱子屈曲近似变形形状，将其对应的弯矩图与单位荷载作用下常用的弯矩图进行积分，推导出不同情况下的图乘系数。

（1）两端固接其中一端有侧移的压杆[106]

如图3.2（a）所示两端固接的压杆在轴力P作用下发生屈曲，最大侧移量为δ。由梁柱微分方程以及边界条件x=0、y=y′=0，x=l、y=δ、y′=0，选取挠曲线方程为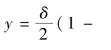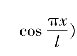，压杆的荷载弯矩为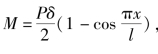端部最大弯矩为Mmax=Pδ。图3.2（b）的弯矩表达式为，最大弯矩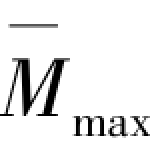=k。将该单位荷载作用弯矩与图3.2（a）压杆屈曲时弯矩积分得：

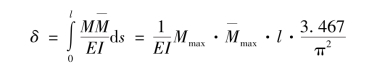
从式（3.5）可以看出，此种情况下的图乘系数

图3.2（c）的弯矩表达式为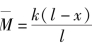，最大弯矩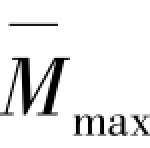=k。将该单位荷载作用弯矩与图3.2（a）压杆屈曲时弯矩积分得：

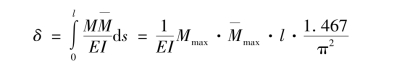
从式（3.5）可以看出，此种情况下的图乘系数

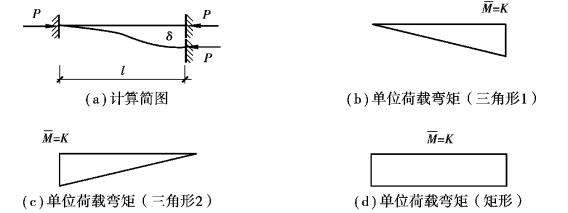
图3.2　压杆变形及单位荷载弯矩图(www.xing528.com)

图3.2（d）的弯矩表达式为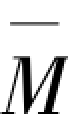=k，最大弯矩为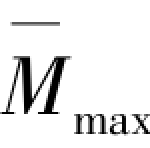=k，将该单位荷载作用弯矩与图3.2（a）压杆屈曲时弯矩积分得：

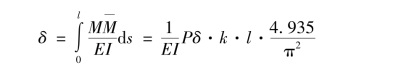
从式（3.5）可以看出，此种情况下的图乘系数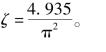

（2）一端固接一端铰接的压杆

如图3.3（a）所示一端固接一端铰接的压杆在轴力P作用下发生屈曲，最大侧移量为δ。由梁柱微分方程以及边界条件x=0、y=y″=0，x=l、y=δ、y′=0，选取挠曲线方程为y=δsin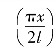，压杆的荷载弯矩为，右端部最大弯矩为Mmax=Pδ。

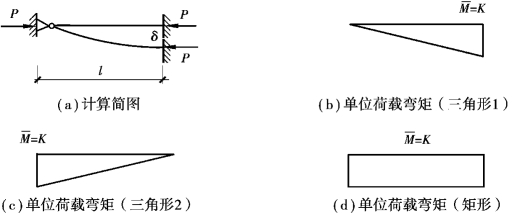
图3.3　压杆变形及单位荷载弯矩图

图3.3（b）的弯矩表达式为，最大弯矩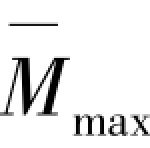=k。将该单位荷载作用弯矩与图3.3（a）压杆屈曲时弯矩积分得：

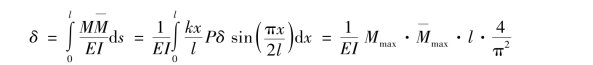
从式（3.5）可以看出，此种情况下的图乘系数

对于图3.3（c）、图3.3（d）及其他不同边界条件的压杆均可按照上述方法进行推导，在此不再一一列出，将不同情况下的常用图乘系数汇总列于表3.1。

表3.1　弯矩图乘系数ζ

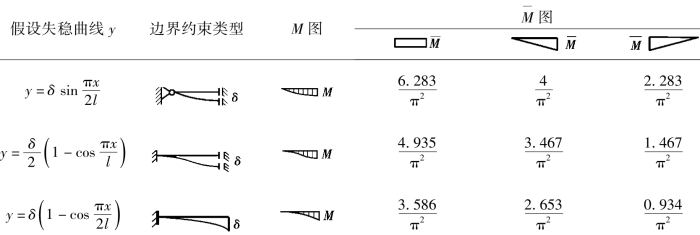
挠度法可扩展运用到杆系结构，如有侧移的框架结构，实际上就是计算框架各层的侧移。为此，首先要假设框架失稳曲线，由此可计算对应于失稳曲线二阶弯矩M，然后分别在各楼层处施加单位荷载并计算其单位荷载弯矩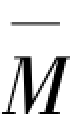，最后两个弯矩图进行图乘计算求出各楼层的侧移，进而求得框架临界力。