挠度法的基本原理是将求临界力转化为求特殊点的挠度，从而极大简化计算。其过程是：首先假设失稳变形曲线，求出轴压力在变形曲线上产生的二阶弯矩；然后求最大弯矩处的挠度，便可得到临界力。这样，挠度法便可扩展运用到杆系结构，比如有侧移的框架结构，实际上就是计算框架各层的侧移，为此，首先要假设框架失稳曲线，由此可计算对应于失稳曲线二阶弯矩M，然后分别在各楼层处施加单位荷载并计算其单位荷载弯矩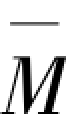
，最后进行图乘计算各楼层的侧移，进而求得框架临界力。
图3.1（a）—（c）分别假设了3种失稳变形曲线（正弦、抛物线和平直线）引起的二阶弯矩，在最大变形处施加单位荷载[图3.1（d）]，现分别求3种情况的挠度。
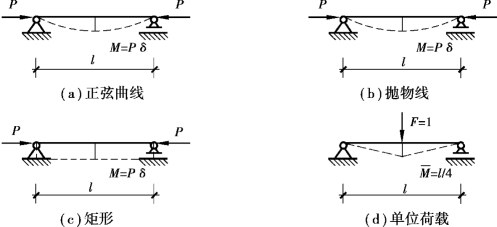
图3.1 两端铰接压杆挠度法计算简图
①令简支梁屈曲时跨中挠度为δ，假定简支梁变形为正弦曲线，其挠曲线变形方程取为y=δsin（πx/l）[图3.1（a）]，在轴力P作用下的弯矩为：M=Py=Pδsin（πx/l），经复核满足边界条件；撤去轴力在简支梁跨中施加单位荷载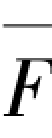
[图3.1（d）]，其弯矩为：
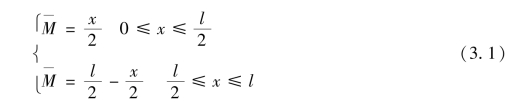
将简支梁图3.1（a）、图3.1（d）下的弯矩图进行积分可得到简支梁跨中的挠度为：
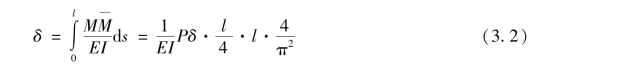(www.xing528.com)
将式（3.2）左右两侧跨中挠度δ消掉，可得出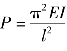
，即为该简支梁轴向荷载作用下的临界荷载，由于假定的挠曲线方程为其屈曲变形的精确形状，相应得到了精确临界荷载。
②假定简支梁变形为二次抛物线，取其挠曲线变形方程取为y=4δx（l-x）/l2[图3.1（b）]；将简支梁图3.1（b）、图3.1（d）下的弯矩图进行积分可得到简支梁跨中的挠度为：
将式（3.3）左右两侧跨中挠度δ消掉，可得临界荷载：
，该值与式（3.2）所求得精确解比值为0.973，误差为2.7%。
③假定简支梁变形为一矩形，其全长挠度变形值均为δ，挠曲线变形方程取为y=δ[图3.1（c）]；将简支梁图3.1（c）、图3.1（d）下的弯矩图进行积分可得到简支梁跨中的挠度为：
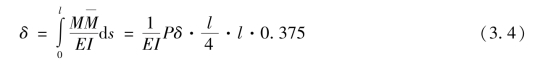
消去δ求得临界力为：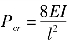
，该值与精确解相比，误差为19%。
这里可以看到：即便假设的失稳变形曲线与精确解相差甚远，极为不合理，得到的临界力与精确解也并不是想象中的那么大。换句话说，选取偏差极大的失稳曲线，并没有导致极大的临界力误差，挠度法对假定的失稳变形曲线精度要求不是很高。从以上3种情况可以看出：选用的挠曲线函数越接近真实屈曲变形曲线，得到的临界力越接近精确解。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
