框架及框剪结构稳定性验证与解析计算方法

通过下面2个算例来实际运用无支撑自由侧移类型下受压柱临界内外刚度比系数α求解柱计算长度系数。用本书方法和规范法进行计算和比较，同时也用有限元ANSYS进行了计算，以便对两种方法的计算结果进行比较。

例题3：无支撑自由侧移框架（底端铰接）

图2.9所示为一自由侧移门式框架，l=600 cm，b=900 cm，梁柱断面均为HW-300×300×10×15，Ix=20 500 cm4，E=2.06×104kN/cm2，求柱的临界力和计算长度系数。

（1）本书方法求解

①由计算简图确定梁柱线刚度比：R1=0.667，R2=0。

②由式（2.22）可求出柱抗侧刚度：K0=3.352 kN/cm；由式（2.26）可求得柱内外刚度比系数：α=1.091。

③由式（2.7）求得柱临界力Pcr=1 745和柱计算长度系数μ=2.576。

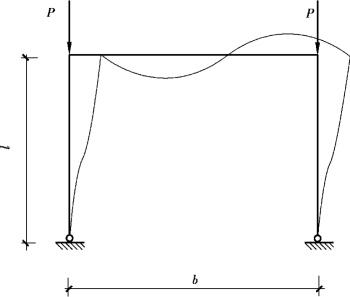
图2.9　例题3计算简图

（2）规范法求解

根据计算简图确定梁柱线刚度比：R1=0.667，R2=0；查规范附录表E.0.2求得：柱临界力Pcr=1 750 kN和柱计算长度系数μ=2.572。

（3）有限元ANSYS求解

ANSYS求解时梁柱建模均采用简单的梁单元beam3，节点均为刚接，材料为弹性，即进行的计算是弹性屈曲分析（图2.10）。采用有限元ANSYS弹性屈曲分析求得：柱临界力Pcr=1 776 kN和柱计算长度系数μ=2.553。

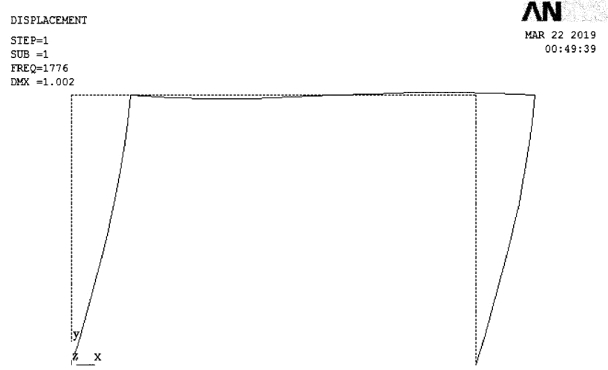
图2.10　屈曲变形模态图

将本书方法、规范法和有限元ANSYS的计算结果归纳在表2.4中，以便对3种方法的计算结果进行比较。

表2.4　柱稳定承载力及计算长度系数对比结果

(www.xing528.com)

从表2.4可以看出，本书方法计算结果与ANSYS对比误差很小，在2%以内，表明采用本书方法计算自由侧移框架柱临界力和计算长度系数的准确性较高。

例题4：无支撑自由侧移框架（底端固接）

图2.11所示钢框架，l=400 cm，b=600 cm，梁柱断面均为HW-300×300×10×15，Ix=20 500 cm4，E=2.06×104kN/cm2，求柱的临界力和计算长度系数。

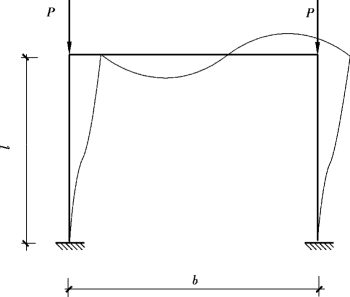
图2.11　例题4计算简图

（1）本书方法求解

①由计算简图确定梁柱线刚度比：R1=0.667，R2=∞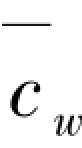，=0。②由式（2.22）求得受压柱抗侧刚度：K0=49.055 kN/cm；由式（2.26）可求得柱内外刚度比系数：α=1.138。

③由式（2.7）求得柱临界力Pcr=17 247和柱计算长度系数μ=1.229。

（2）规范法求解

根据计算简图确定梁柱线刚度比：R1=0.667，R2=∞；查规范按照无支撑自由侧移框架柱根据附录表E.0.2求得：柱临界力Pcr=16 539 kN和柱计算长度系数μ=1.255。

（3）有限元ANSYS求解

有限元ANSYS弹性屈曲分析（图2.12）求得：柱临界力Pcr=17 430 kN和柱计算长度系数μ=1.223。

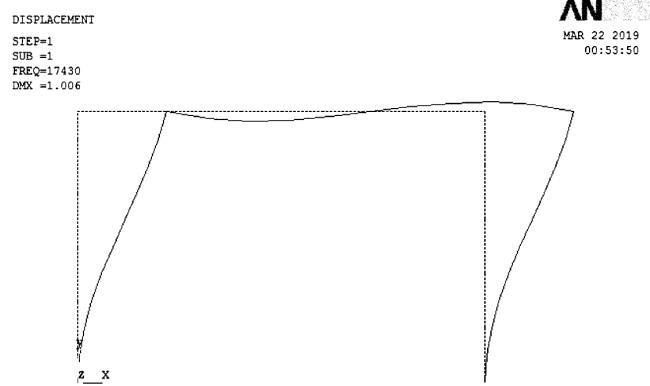
图2.12　屈曲变形模态图

将本书方法、规范法和有限元ANSYS的计算结果归纳在表2.5中，以便对3种方法的计算结果进行比较。

表2.5　柱稳定承载力及计算长度系数对比结果

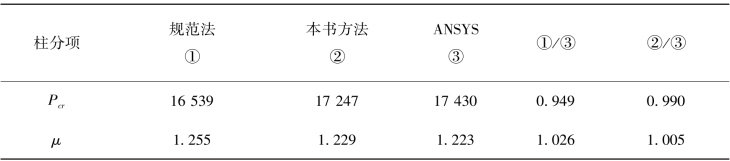
从表2.5可以看出，本书方法计算结果与ANSYS对比误差很小，在5%以内，表明本书方法计算自由侧移框架柱临界力和计算长度系数的准确性。