受压柱侧移类型-框架及框剪结构整体稳定性的解析计算方法研究

计算长度系数法的精度取决于受压柱分离过程中边界条件的选取，分离时除要考虑结构的侧向变形（有侧移和无侧移）外，还要考虑与该柱相连的约束情况，分离柱的两端可能还带有不同的约束。为了更接近从整体结构中分离受压柱的约束情况，将图2.1（c）中弹簧用更一般约束情况的受压柱替换，结构中绝大部分的柱端约束都可用3个或两个弹簧来模拟，如图2.2所示的受压柱，柱端带有3个弹簧，其转动刚度和侧移刚度分别用c1、c2和cw表示。

该柱的平衡微分方程属于经典压杆平衡微分方程，可写为：

式中　，是柱的无量纲特征系数。

方程（2.3）的通解为：

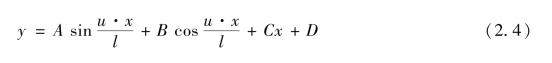
存在如下边界条件：

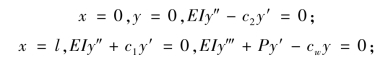
式中，c1、c2和cw均为弹簧刚度，为了更具有代表性和通用性，引入相对刚度，定义R1=c1/（6ic），R2=c2/（6ic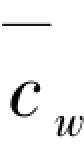），=（cwl2）/ic，ic为柱的线刚度；用第一个边界条件得到：D=-B，由此可以消掉一个未知量，将前述边界条件代入式（2.4）可得：

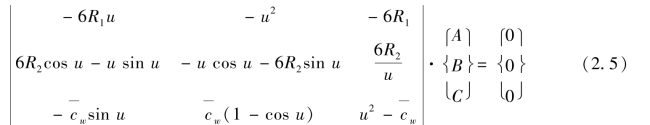
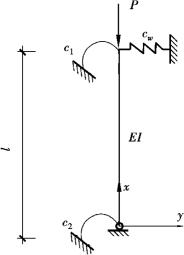
图2.2　三弹簧约束受压柱计算简图

系数A、B、C全为零时，可满足方程（2.5），此为失稳前的平衡状态，即受压柱未发生侧移，因此需要寻找失稳后的平衡模态，要满足这个条件，需方程（2.5）的系数行列式等于零，由此可得三弹簧受压柱的稳定特征方程[102]：(https://www.xing528.com)

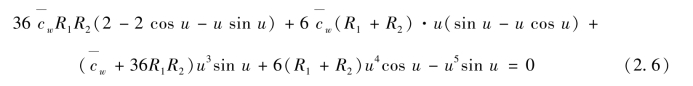
该特征方程几乎包含了柱所有的边界约束情况，通过变化R1，R2和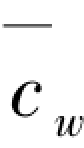的取值可以实现各种不同的边界约束条件。

通过变化相对刚度R1、R2的取值可以实现杆端不同的约束：

①R1=0或R2=0表示柱端约束条件为铰接约束。

②当R1=∞或R2=∞表示柱端约束条件为固定端约束。

通过变化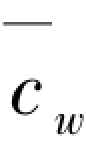的取值可以模拟实现不同侧移类型受压柱：

①当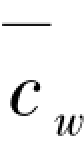=∞时，为强支撑无侧移的受压柱。

②当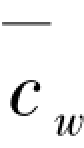=0时，为无支撑自由侧移的受压柱。

③当0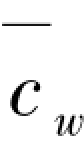＜＜∞时，为弹性支撑有弹性侧移的受压柱。稳定特征方程（2.6）虽然可以精确求解各种类型受压柱的计算长度系数，但其属于多变量的超越方程，直接求解柱计算长度系数是十分困难的。因此，有必要寻找确定受压柱计算长度系数的简便算法。根据受压柱在临界状态下柱外刚度将内刚度削弱为零的这一原理，由式（2.2）可以得出受压柱临界力：

由于受压柱临界力，根据式[2.7（a）]可以计算出柱计算长度系数：

从式（2.7）可以看出，在确定了受压柱临界内外刚度比系数α后，只要求得受压柱的内刚度K0，即为受压柱的一阶抗侧刚度，就可得到受压柱临界力和计算长度系数，这样就可将求解受压柱计算长度系数的二阶问题转化为计算受压柱一阶抗侧刚度，避免了求解复杂的超越方程，使得求解大大简化。