解析框架结构整体稳定性计算方法

单独的摇摆柱自身是不稳定的，也是无法承载的，只有依附在稳定结构（简称为主结构）上，靠主结构提供刚度支持来进行承载。“主结构+摇摆柱”在本书中称为扩展结构，主结构的侧移刚度可用一个弹簧来表示，图2.1中扩展结构1和扩展结构2都可利用“弹簧-摇摆柱”模型来表示，不同之处在于：扩展结构1和扩展结构2中的主结构的侧移刚度（弹簧刚度）不同。当扩展结构失稳时，相当于依附在主结构上的摇摆柱将主结构刚度削弱为零，这种受力特性可用图2.1（c）弹簧-摇摆柱模型进行模拟。

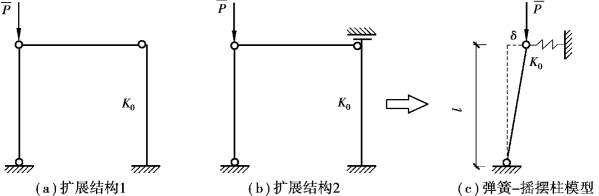
图2.1　弹簧-摇摆柱模型

图2.1（c）弹簧-摇摆柱模型中弹簧刚度为K0，即为主结构的抗侧刚度，在摇摆柱柱顶施加荷载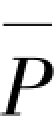，产生侧移δ，对下端取矩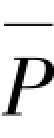：δ-K0δ·l=0，可得出弹簧-摇摆柱结构临界状态表达式：

式（2.1）物理意义为外荷载对弹簧刚度的削弱程度，当处于临界平衡状态时弹簧刚度被削弱至零而失稳。该式中K0仅与弹簧的固有参数有关，与外荷载无关，随着结构形式确定而确定，是结构的固有特征，称为内刚度；取扩展结构临界力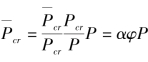（Pcr为主结构的临界力，P为主结构作用的外荷载），则存在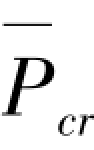/h=αφP/l，P/l与K0量纲相同，称为外刚度，用KP表示。外刚度KP主要与所施加外力有关，随着外荷载P的增大而增大，当外荷载P=Pcr时，对应的外刚度Pcr/l称为临界外刚度，用KPcr表示。因此，式（2.1）临界平衡方程可用结构内外刚度表达为：(www.xing528.com)

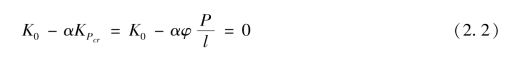
式中　α———临界内外刚度比系数，即为K0/KPcr，计算值等于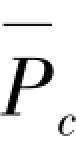r/Pcr，图2.1（c）弹簧-摇摆柱模型中α=1.0；

φ———结构的临界因子，数值上φ=Pcr/P，当结构处于临界状态时φ=1.0。

①图2.1（a）所示下端固定、上端自由的轴压杆，当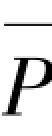→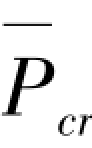，K0→0时，α=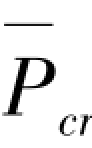/Pcr=1.216；Pcr为图2.1（a）所示主结构轴压杆的临界力。

②图2.1（b）所示两端固定但可相对侧移的轴压杆，当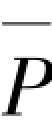→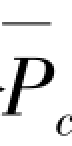r，K0→0时，α=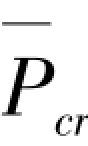/Pcr=1.216。