【摘要】:理想受压柱在实际上是不存在的,实际工况中的柱子可能存在初始缺陷,轴力的作用点也可能存在初始偏心,因而绝大部分的柱子都是偏心受压柱[图1.2],属于极值点失稳,其极限荷载也称为失稳极限荷载,也称为压溃荷载[3]。图1.3示意了偏心受压柱的一阶弹性、二阶弹性和二阶弹-塑性分析3种情况的荷载-变形曲线。第3种情况:采用二阶分析且材料为弹塑性时,曲线的极限承载力大为降低,曲线由上升段和下降段组成,极限荷载位于极值点。
理想受压柱在实际上是不存在的,实际工况中的柱子可能存在初始缺陷,轴力的作用点也可能存在初始偏心,因而绝大部分的柱子都是偏心受压柱[图1.2(b)],属于极值点失稳(第二类失稳),其极限荷载也称为失稳极限荷载,也称为压溃荷载[3]。
图1.3示意了偏心受压柱的一阶弹性、二阶弹性和二阶弹-塑性分析3种情况的荷载-变形曲线。当N=0时,柱子存在初始偏心距(e1),3种曲线的挠度变形都是从e1开始。这3种情况分别是:
第1种情况:采用一阶弹性分析时,荷载作用与变形之间是线性关系,所以在图1.3中为一条直线。
第2种情况:采用二阶弹性分析时,荷载作用和变形不再是线性关系而是非线性关系,当材料为弹性时,曲线趋近于屈曲荷载。(https://www.xing528.com)
第3种情况(极值点失稳):采用二阶分析且材料为弹塑性时,曲线的极限承载力大为降低,曲线由上升段和下降段组成,极限荷载位于极值点。从N=0开始,变形随着荷载作用的增大而增大,变形逐渐进入塑性阶段,曲线斜率下降,变形快速增加,当荷载作用达到极限值(极值点),变形曲线进入下降段,荷载必须下降才能维持内力和外力的平衡。这种变化特性也被称为量变失稳[5]。
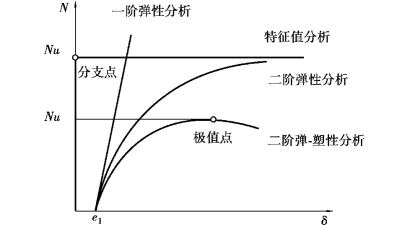
图1.3 柱的荷载-挠度曲线
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




