资金时间价值及计算方法

考点汇集

考点1 现金流量与资金的时间价值

一、现金流量

（一）含义

现金流入CI_t：在某一时点t流入系统的资金。

现金流出CO_t：在某一时点t流出系统的资金。

净现金流量NCF或（CI-CO）_t：同一时点上的现金流入与现金流出之差。

现金流入量、现金流出量、净现金流量统称为现金流量。

（二）现金流量图

1.概念及作用

现金流量图是一种反映经济系统资金运动状态的图式。运用现金流量图，可以全面、形象、直观地表示现金流量的三要素：大小（资金数额）、方向（资金流入或流出）和作用点（资金的发生时间点），如下图所示。

现金流量图

2.现金流量图的绘制规则

（1）横轴为时间轴，0表示时间序列的起点，n表示时间序列的终点。轴上每一间隔代表一个时间单位（计息周期），可取年、半年、季或月等。整个横轴表示的是所考察的经济系统的寿命期。

（2）与横轴相连的垂直箭线代表不同时点的现金流入或现金流出。在横轴上方的箭线表示现金流入（收益），在横轴下方的箭线表示现金流出（费用）。

（3）垂直箭线的长短要能适当体现各时点现金流量的大小，并在各箭线上方（或下方）注明现金流量的数值。

（4）垂直箭线与时间轴的交点即为现金流量发生的时点（作用点）。

二、资金的时间价值

（一）概念

（1）资金在运动中，会随着时间的推移而变动。变动的这部分资金就是原有资金的时间价值。

（2）由于资金时间价值的存在，不同时间上发生的现金流量无法直接进行比较。只有通过一系列的换算，在同一时点上进行对比，才能符合实际客观情况。

（二）利息与利率

利息是资金时间价值的一种重要表现形式。通常，用利息额作为衡量资金时间价值的绝对尺度，用利率作为衡量资金时间价值的相对尺度。

1.利息

在借贷过程中，债务人支付给债权人超过原借贷款金额（常称为本金）的部分，就是利息，即

I=F-P （4-1）

式中 I——利息；

F——还本利息总额；

P——本金。

在工程经济分析中，利息常常被看作是资金的一种机会成本。从投资者角度来看，利息体现为对放弃现期消费的损失所作的必要补偿。在工程经济分析中，利息是指占用资金所付的代价或者是放弃使用资金所得的补偿。

2.利率

利率是指在单位时间内（如年、半年、季、月、周、日等）所得利息额与借贷款金额（本金）之比，通常用百分数表示，即

式中 i——利率；

I_t——单位时间内的利息；

P——借款本金。

用于表示计算利息的时间单位称为计息周期，通常为年、半年、季、月、周或日。

3.影响利率的主要因素

（1）社会平均利润率。利率随社会平均利润率的变化而变化。通常情况下，平均利润率是利率的最高界限。因为如果利率高于利润率，无利可图就不会有人去借款。

（2）借贷资本的供求情况。在平均利润率不变的情况下，借贷资本供过于求，利率便下降；反之，供不应求，利率便上升。

（3）借贷风险。借出资本要承担一定的风险，风险越大，利率也就越高。

（4）通货膨胀。通货膨胀对利息的波动有直接影响，资金贬值往往会使利息无形中成为负值。

（5）借出资本的期限长短。贷款期限长，不可预见因素多，风险大，利率就高；反之，贷款期限短，不可预见因素少，风险小，利率就低。

考点2 利息计算方法

一、单利计算

单利是指在计算利息时，仅用最初本金来加以计算，而不计入在先前利息周期中所累积增加的利息，即通常所说的“利不生利”的计息方法，其计算公式如下：

I_t=Pi_d （4-3）

式中 I_t——第t个计息周期的利息额；

P——本金；

i_d——计息周期单利利率。

设I_n代表n个计息周期所付或所收的单利总利息，则有

由式（4-4）可知，在以单利计息的情况下，总利息与本金、利率以及计息周期数成正比。而n期末单利本利和F等于本金加上利息，即

F=P+I_n=P（1+ni_d） （4-5）

（1+ni_d）称为单利终值系数。

利用式（4-5）计算本利和F时，要注意式中n和i_d反映的时期要一致。例如，若i_d为年利率，则n应为计息的年数；若i_d为月利率，则n应为计息的月数。

单利没有反映资金随时都在“增值”的规律，即没有完全反映资金的时间价值（工程经济分析中使用较少）。

二、复利计算

复利是指将其上期利息结转为本金来一并计算的本期利息，即通常所说的“利生利”“利滚利”的计息方法，其计算公式为

I_t=iF_t-1 （4-6）

式中 I_t——第t年末利息；

i——计息周期利率；

F_t-1——第（t-1）年末复利本利和。

第t年末复利本利和F_t的表达式为

F_t=F_t-1（1+i）=F_t-2（1+i）²=…=P（1+i）ⁿ （4-7）

同一笔借款，在利率和计息周期均相同的情况下，用复利计算出的利息金额数比用单利计算出的利息金额数大。

复利反映利息的本质特征，复利计息比较符合资金在社会生产过程中运动的实际状况。

复利计算有间断复利和连续复利之分。按期（年、半年、季、月、周、日）计算复利的方法称为间断复利（即普通复利）；按瞬时计算复利的方法称为连续复利。在实际应用中，一般均采用间断复利。

考点3 等值计算

一、影响资金等值的因素

由于资金的时间价值，金额相同的资金发生在不同时间会产生不同的价值；反之，不同时点金额不等的资金，在时间价值的作用下，却可能具有相等的价值。

影响资金等值的因素有：资金的多少、资金发生的时间及利率（或折现率）的大小。其中，利率是一个关键因素，在等值计算中，一般是以同一利率为依据的。

二、等值计算方法

（一）图形及公式

一次支付现金流量图

等额系列现金流量示意图a）

等额系列现金流量示意图b）

（二）计算过程

1.一次支付

一次支付又称整付，是指所分析系统的现金流量，无论是流入或是流出，分别在时点上只发生一次。

（1）终值计算。已知P求F，一次支付n年末复本利和F的计算公式为

F=P（1+i）ⁿ （4-8）

式中 i——计息周期复利率；

n——计息周期数；

P——现值（即现在的资金价值或本金，Present Value），是指资金发生在（或折算为）

某一特定时间序列起点时的价值；

F——终值（n期末的资金价值或本利和，Future Value），是指资金发生在（或折算为）(www.xing528.com)

某一特定时间序列终点时的价值。

（1+i）n称为一次支付终值系数，用（F/P，i，n）表示，则

F=P（F/P，i，n） （4-9）

式中，括号内斜线左侧的符号表示所求的未知数，斜线右侧的符号表示已知数。（F/P，i，n）就表示已知P、i和n的情况下求解F的值。可查复利表进行计算。

（2）现值计算。已知F求P，由式（4-8）即可求出现值P，即

P=F（1+i）-ⁿ （4-10）

（1+i）-ⁿ称为一次支付现值系数，用符号（P/F，i，n）表示。在工程经济中，一般是将未来时刻的资金价值折算为现在时刻的价值，该过程称为折现或贴现，所使用的利率称为折现率或贴现率。因此，（1+i）-ⁿ或（P/F，i，n）也可称为折现系数或贴现系数，式（4-10）常写成

P=F（P/F，i，n） （4-11）

2.等额支付系列情形

多次支付是指现金流量在多个时点发生，而不是集中在某一个时点上。如果用A_t表示第t期末发生的现金流量（可正可负），用逐个折现的方法，可将多次现金流量换算成现值，即

或

同理，也可将多次现金流量换算成终值：

或

式中 A——年金，发生在（或折算为）某一特定时间序列各计息期末（不包括零期）的等

额资金序列的价值。

等额系列现金流量的复利计算方法如下：

（1）终值计算。已知A求F。由式（4-14）展开得

式中，称为等额系列终值系数或年金终值系数，用符号（F/A，i，n）表示，式（4-16）又可写成

F=A（F/A，i，n） （4-17）

（2）现值计算。已知A求P。由式（4-10）和式（4-16）得

式中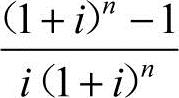，称为等额系列现值系数或年金现值系数，用符号（P/A，i，n）表示，则式（4-18）又可写成

P=A（P/A，i，n） （4-19）

（3）资金回收计算。已知P求A。等额系列资金回收计算是等额系列现值计算的逆运算，故由式（4-18）可得

式中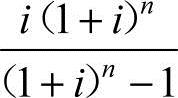，称为等额系列资金回收系数，用符号（A/P，i，n）表示，则式（4-20）又可写成

A=P（A/P，i，n） （4-21）

（4）偿债基金计算。已知F求A。偿债基金计算是等额系列终值计算的逆运算，故由式（4-16）可得

式中，称为等额系列偿债基金系数，用符号（A/F，i，n）表示，则式（4-22）又可写成

A=F（A/F，i，n） （4-23）

3.工程经济分析时的注意事项

工程经济分析中，现值比终值使用更为广泛。在工程经济分析时应当注意以下两点：

（1）正确选取折现率。折现率是决定现值大小的一个重要因素，必须根据实际情况灵活选用。

（2）注意现金流量的分布情况

1）从收益角度来看，获得的时间越早，数额越大，其现值就越大。因此，应使建设项目早日投产，早日达到设计生产能力，早获收益，多获收益，才能达到最佳经济效益。

2）从投资角度来看，投资支出的时间越晚、数额越小，其现值就越小。因此，应合理分配各年投资额，在不影响项目正常实施的前提下，尽量减少建设初期投资额，加大建设后期投资比重。

三、名义利率与有效利率

（一）名义利率

名义利率r是指计息周期利率i乘以一个利率周期内的计息周期数m所得的利率周期利率。即

r=im （4-24）

计算名义利率时忽略了前面各期利息再生利息的因素，这与单利的计算相同。通常所说的利率周期利率都是名义利率。

（二）有效利率

有效利率是指资金在计息中所发生的实际利率，包括计息周期有效利率和利率周期有效利率两种情况。

1.计息周期有效利率

2.利率周期有效利率

若用计息周期利率来计算利率周期有效利率，并将利率周期内的利息再生利息因素考虑进去，这时所得的利率周期利率称为利率周期有效利率（又称利率周期实际利率）。

已知利率周期名义利率r，一个利率周期内计息m次，则计息周期利率为i=r/m，在某个利率周期初有资金P，则利率周期终值F的计算式为

利率周期有效利率计算的现金流量图

根据利息的定义可得该利率周期的利息I为

再根据利率的定义可得该利率周期的有效利率i_eff为

在名义利率r一定时，每年计息期数m越多，i_eff与r相差越大。

真题实战

1.某企业从银行借入1年期的短期借款500万元，年利率12%，按季度计算并支付利息，则每季度需支付利息（ ）万元。【2012年单选真题】

A.15.00 B.15.15 C.15.69 D.20.00

【答案】A

【解析】本题考查的是复利计算。题目中给定年利率12%，即年名义利率，则可知季度利率为3%，所以，每季度需支付利息为：500×3%=15.00（万元）。

2.影响利率的因素有多种，通常情况下，利率的最高界线是（ ）。【2013年单选真题】

A.社会最大利润率 B.社会平均利润率

C.社会最大利税率 D.社会平均利税率

【答案】B

【解析】在通常情况下，平均利润率是利率的最高界线。

3.某工程建设期2年，建设单位在建设期第1年初和第2年初分别从银行借入700万元和500万元，年利率8%，按年计息。建设单位在运营期前3年每年末等额偿还贷款本息，则每年应偿还（ ）万元。【2014年单选真题】

A.452.16 B.487.37 C.526.36 D.760.67

【答案】C

【解析】本题考查等值计算。A=[700×（F/P，8%，2）+500×（F/P，8%，1）]×（A/P，8%，3）=526.36。

4.某企业年初从银行贷款800万元，年名义利率10%，按季度计算并支付利息，则每季度末应支付利息（ ）万元。【2014年单选真题】

A.19.29 B.20.00 C.20.76 D.26.67

【答案】B

【解析】本题考查的是名义利率。每季度末利息=800×（10%/4）=20万元。预测试题

1.现金流量图可以全面、直观地反映经济系统的资金运动状态，其中现金流量的三大要素包括（ ）。

A.现金流入的大小、方向和时间点 B.投入现金的额度、时间和回收点

C.现金流量的大小、方向和作用点 D.现金流出的额度、方向和时间点

2.在工程经济分析中，利息是指投资者（ ）。

A.因通货膨胀而付出的代价 B.使用资金所得的预期收益

C.使用资金的平均利润率 D.占用他人的资金而付出的代价

3.下列关于利息和利率的说法中，不正确的是（ ）。

A.利息是占用资金所付出的代价 B.利息是衡量资金时间价值的尺度

C.利率的高低取决于平均投资利润率的高低 D.利息能够促进企业加强经济核算

4.某公司向银行借款2000万元，年复利利率为10%。若公司向银行所借的本金和产生的利息均在5年后一次向银行支付，则支付本利和为（ ）万元。

A.3000 B.3100 C.3222 D.4000

5.某项目建设期为2年，建设期内每年初分别贷款600万元和900万元，年利率为10%。运营期前5年内每年末等额偿还贷款本利，则每年应偿还贷款本利（ ）万元。

A.343.20 B.395.70 C.411.52 D.452.68

参考答案

恭喜您顺利完成第2周第6天的学习任务！

第2周 第7天 日期：2015年____月____日

学习内容：第四章第二节