水文数据处理方面的Excel应用示例

1.流域产流量计算

江苏省连云港西双湖水库流域有阿湖、双店和麦坡3个雨量站。用泰森多边形法求得它们的权重系数分别为0.009，0.732和0.259。产流量计算采用《江苏省暴雨洪水图集》中的地区综合成果《苏北旱地次降雨径流关系图》，其形式为P＋Pa～R相关曲线，其相应的数学模型为：

式中：Cp，Ci为模型参数。

已知西双湖水库流域的Cp＝20，Ci＝75，流域的最大蓄水量为75mm。

（1）输入数据。阿湖、双店和麦坡3个雨量站的权重系数和相应雨量数据输入Excel的有关单元格中，见图7.55中的单元格B2：D10。

（2）计算面平均雨量。在E3单元格输入公式“＝B3*＄B＄2＋C3*＄C＄2＋D3*＄D＄2”，回车确定。将公式复制到E4：E10，即得到各日的面平均雨量，计算结果见图7.55中的单元格E3：E10。

（3）计算前期影响雨量。前期影响雨量计算公式为：

式中：Pa，t＋1为第t＋1日的前期影响雨量，mm；Pa，t为第t日的前期影响雨量，mm；xt为第t日的降雨量，mm；K为土壤含水量消退系数；Im为流域最大蓄水量，mm。

根据式（7.8）及该流域的Im值计算每日的前期影响雨量Pa值。在图7.56中的F4单元格中输入公式：＝IF（0.9*（E3＋F3）＞75，75，0.9*（E3＋F3）），回车确定，将公式复制到F4：F10，各日的前期影响雨量Pa值见单元格F3：F10。

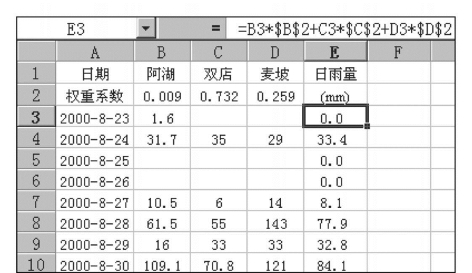
图7.55　西双湖水库流域产流量计算表1

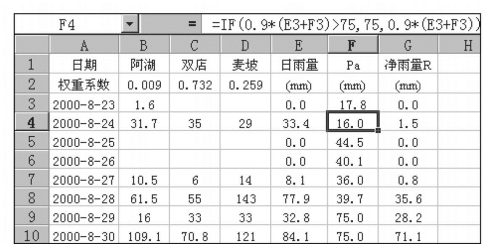
图7.56　西双湖水库流域产流量计算表2

（4）净雨量计算。净雨量计算的公式采用上述式（7.7），且有当计算的净雨量R大于日雨量P时，R＝P。

1）方法1。在单元格G3中输入公式“IF（（（E3＋F3－20）^3＋75^3）^（1/3）－75＞E3，E3，（（E3＋F3－20）^3＋75^3）^（1/3）－75）”，回车确定，将公式复制到G4：G10，净雨量如图7.57所示。

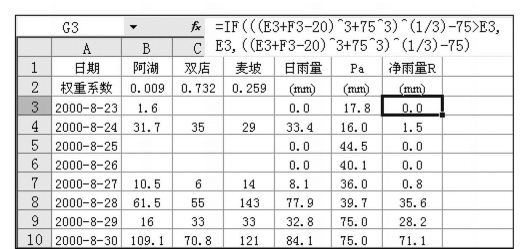
图7.57　西双湖水库流域产流量计算表3

2）方法2。计算净雨量也可以用自定义函数的方法。自定义函数如图7.58所示。

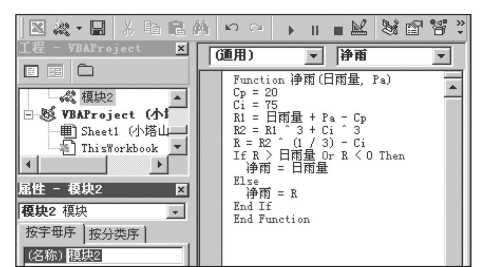
图7.58　西双湖水库产流量计算自定义函数

在图7.59中的单元格H3中输入公式“＝净雨（E3，F3）”，回车确定，将公式复制到H4：H10，即净雨量过程。对比G列中用IF函数计算的结果，两者相同。

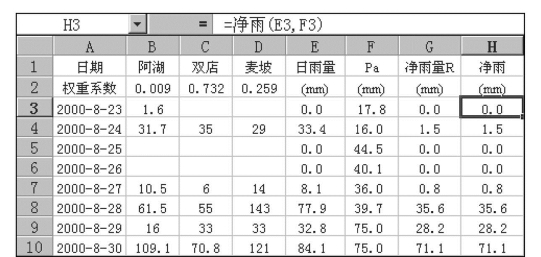
图7.59　西双湖水库流域产流量计算表4

2.Excel的图表应用

Excel在图表制作方面也具有良好的功能，通过绘制大断面图的实例简单介绍利用Excel制作图表的方法。

2002年高港闸站大断面部分数据见图7.60，现欲绘制高港闸站上游大断面图和水位面积关系曲线。需要说明的是因为数据较多，为节省篇幅，图7.60中仅列出部分数据。

（1）取菜单中的“插入—图表—XY散点图”，再选择“子图表类型（T）”中的第3图，如图7.61所示。

（2）单击“下一步”后，转入图7.62。

（3）在数据区域（D）中键入数据区域范围，本例数据区域为B3：C93，转入图7.63。

（4）单击“下一步”后，转入图7.64，在图表标题栏中输入“高港闸（闸上游）站实测大断面图”、数值（X）轴栏中输入“起点距（m）”、数值（Y）轴栏中输入“河底高程 废黄河口基面（m）”。

图7.60　高港站大断面数据

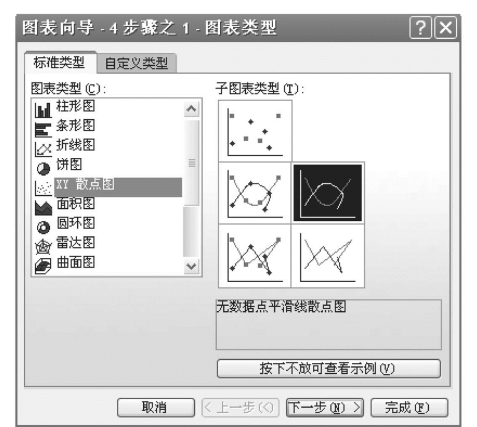
图7.61　Excel的图表应用示例1

（5）单击“完成”，再对图中的坐标轴字体、曲线的颜色、主要和次要网格线等一系列整理，得结果如图7.65所示。

利用如图7.66所示的实测大断面数据，再以类似的步骤，即可绘出高港闸站上游水位面积关系曲线，如图7.67所示。

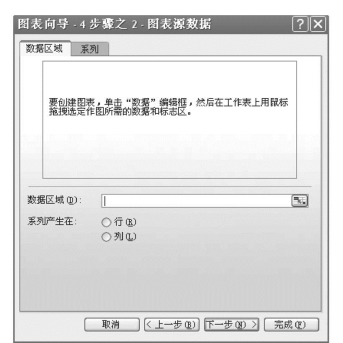
图7.62　Excel的图表应用示例2

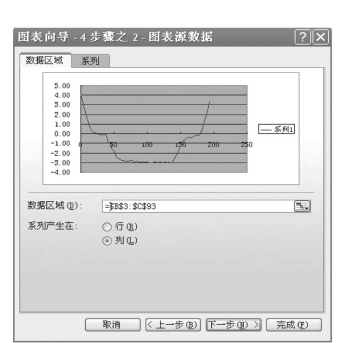
图7.63　Excel的图表应用示例3

图7.64　Excel的图表应用示例4

图7.65　高港闸站大断面图

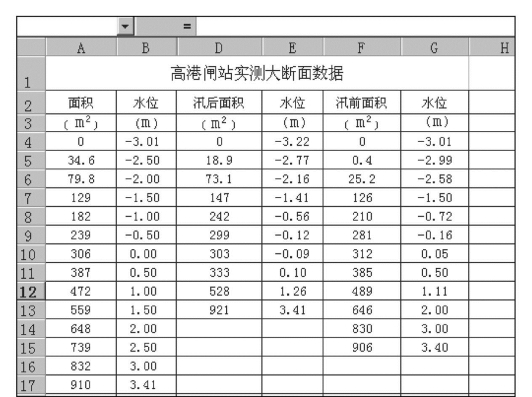
图7.66　高港站大断面数据

图7.67　高港闸站（上游）水位面积关系曲线图

3.断面流量计算表的编制

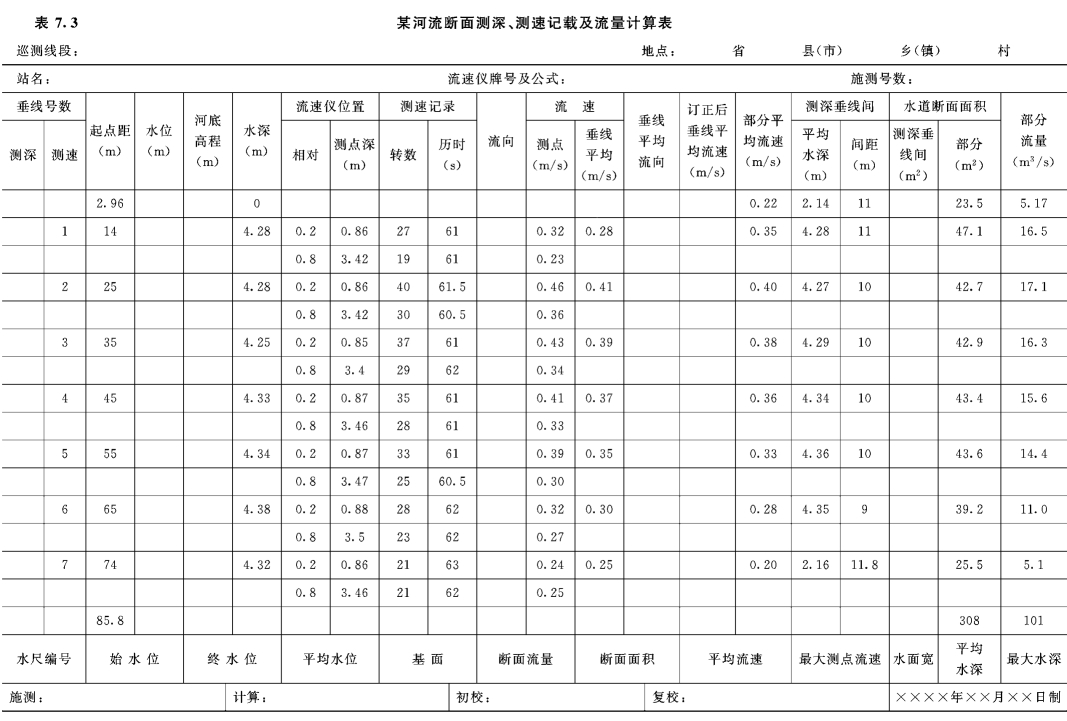
河道断面流量测验大多使用流速仪法和浮标法，都必须有断面测量、流速测量及流量计算三个环节。

（1）断面测量。断面测量的方法是在测流断面上根据河宽和断面的转折变化情况，布设一定数量的测深垂线，测得每条测深垂线与岸上起点桩距间的水平距离（起点距）和水深。

（2）流速测量。天然河道中，普遍采用流速仪测流速。计算公式为：

式中：v为水流速度，m/s；N为旋转器在T秒内的总转数；T为测速历时，s；a，b分别为流速仪常数。

测验时各站根据流量测验方案在规定的测点上测速。

（3）流量计算。各测点的流速测定后，使用专用表格计算断面流量。包括：垂线平均流速计算、部分平均流速计算、部分面积计算、部分流量计算和断面流量计算。除此以外，还要计算许多规定的相关项目。

根据流量测验的步骤，用Excel来编制流量计算表，记录并计算河道断面流量非常方便。

表7.3为某河流断面测深、测速记载及流量计算表，利用Excel的自动重新计算功能，每次只要输入起点距、水位、河底高程和流速仪测速记录等数据，Excel将自动计算垂线平均流速、断面部分平均流速、水道部分断面面积、断面部分流量和过水断面总流量。

4.水文数据的查询及分类汇总

Excel的数据筛选功能，为大量水文数据的查询、数据分析提供了极大方便。现以西双湖水库流域的雨量（1963～2000年）资料为例，说明Excel的数据筛选功能和分类汇总。西双湖水库流域面平均日雨量由阿湖、双店和麦坡3个雨量站用泰森多边形法求得。西双湖水库流域部分年雨量资料如图7.68所示，现要求查询满足某些条件的雨量资料。

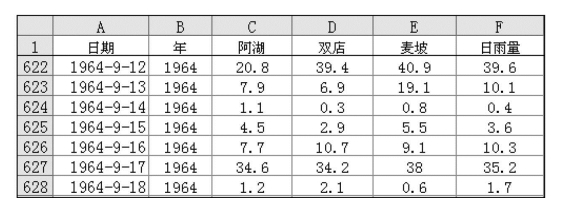
图7.68　西双湖水库流域部分年雨量资料

（1）执行“数据”菜单中的“筛选”命令，在执行“自动筛选”命令后，在数据清单中每一个列标记的右侧将出现一具下拉箭头，如图7.69所示。

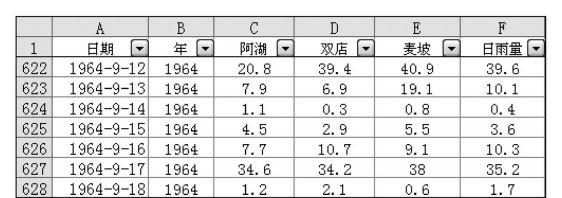
图7.69　数据的查询及分类汇总示例1

（2）按下箭头，会弹出一张下拉列表，其中包括了本字段现有的各个数据。此外，包括了“全部”、“自定义”和“前10个”选项。

（3）如单击“阿湖”字段的小箭头，选择自定义，出现如图7.70所示的对话框。

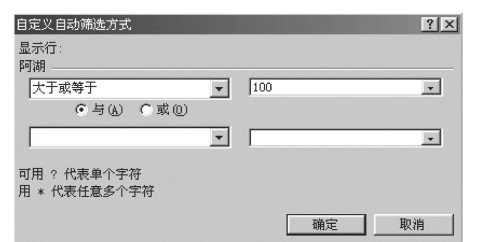
图7.70　数据的查询及分类汇总示例2

在对话框中左上角的列表框中选择“大于或等于”，在其右边的列表框中选择“100”，单击“确定”按钮，就出现阿湖站日雨量大于或等于100mm的记录，如图7.71中C列所示。

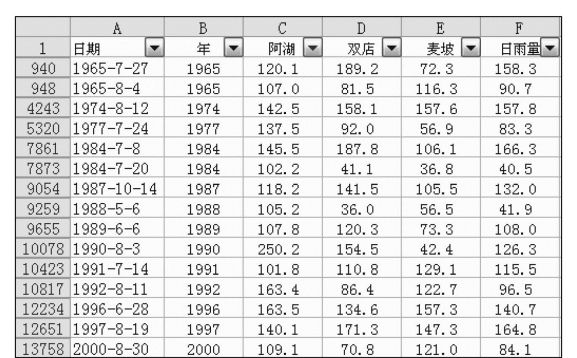
图7.71　数据的查询及分类汇总示例3

图7.72　数据的查询及分类汇总示例4

（4）如果要进一步计算西双湖水库流域1963～2000年的年雨量，可执行“数据”菜单中的“分类汇总”命令，在执行“分类汇总”命令后，出现如图7.72所示的对话框。

（5）在“分 类 字 段（A）”列 表 框 中 选 择“年”，在“汇总方式（U）”列表框中选择“求和”，然后在“选定汇总项（D）”中选择“日雨量”复选框，单击确定，分类汇总的结果如图7.73所示。

在汇总表的左上角的“1”、“2”、“3”按钮代表了分类汇总的层次。

5.数据透视表的应用

数据透视表是一个能够快速合并和比较大量数据的交互式表格，如果要分析相关的总计值，尤其是要对一长串的数字进行求和并对每个数字进行多重比较时，就可以使用数据透视表，通过旋转它的行和列来查看不同源数据的汇总。以西双湖水库流域的雨量资料为例，说明Excel数据透视表的应用，部分雨量资料见图7.68。(www.xing528.com)

（1）从菜单栏的“数据”菜单中选择“数据透视表和数据透视图”，转入图7.74。

（2）出现“数据透视表和数据透视图向导3—步骤1”对话框后，选择“Microsoft Office Excel数 据 列 表 或 数 据 库（M）”和“数 据 透 视 表（T）”，单 击按钮。

图7.73　数据的查询及分类汇总示例5

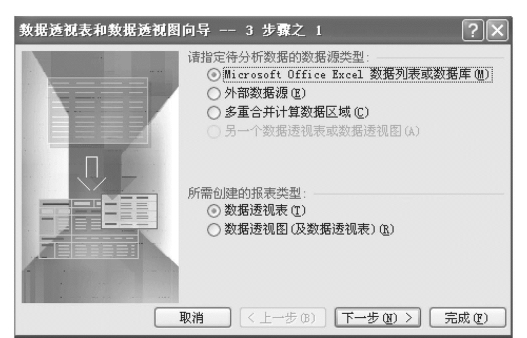
图7.74　数据透视表对话框1

（3）出现“数据透视表和数据透视图向导3—步骤2”对话框后（图7.75），在“选定区域”栏中输入数据的来源范围，本例中的数据区域为A1：F13881，然后单击按钮。

图7.75　数据透视表对话框2

（4）出现“数据透视表和数据透视图向导3—步骤3”对话框后（图7.76），选择“新建工作表”，然后单击按钮。

图7.76　数据透视表对话框3

图7.77　数据透视表对话框4

（5）出现“数据透视表字段列表”工作框后（图7.77），分别拖移年、阿湖、双店、麦坡和日雨量等字段到工作表的行、列、数据区域位置。完成后，可以得相关雨量的分析统计值，阿湖站、双店站、麦坡站年最大日雨量统计、年雨量统计分别见图7.78、图7.79。

（6）更新数据透视表。修改或新增来源数据表的内容时，也可更新数据透视表。更新数据透视表可按以下方法操作：移动鼠标到Sheet工作表修改数据内容，接着切换到数据透视表，单击“更新数据（R）”按钮，统计数据就会随之更新。

6.回归分析

回归分析是水文数据处理中常用的手段，应用极为广泛，此处简要介绍Excel在线性回归分析中的应用，着重通过一元线性回归分析加以说明。

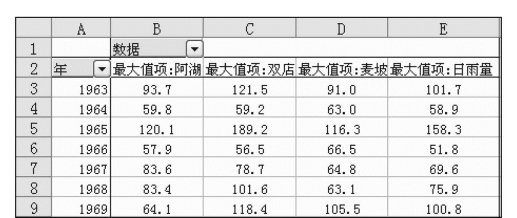
图7.78　阿湖站、双店站、麦坡站年最大日雨量统计

现有相邻流域x和y的同期年径流模数（L/s/km2）的数据资料，见图7.80某相邻流域x和y的同期年径流模数中单元格B2：C12，拟建立y倚x的回归方程，并进行统计检验（α＝0.05）。

图7.79　阿湖站、双店站、麦坡站年雨量统计

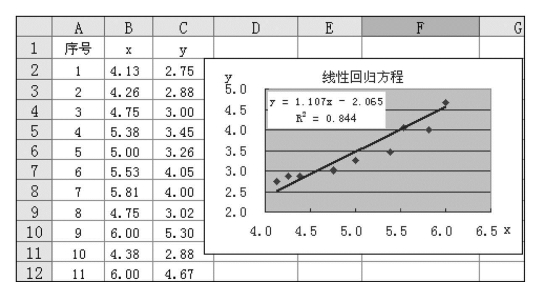
图7.80　某相邻流域x和y的同期年径流模数

使用“分析工具”进行回归分析，其具体步骤如下：

（1）执行“工具（T）/数据分析（D）...”命令，选择“回归”项，见图7.81。

图7.81　回归分析对话框1

（2）按钮，转入图7.82。

（3）在“Y值输入区域”输入＄C＄1：＄C＄12，在“x值输入区域”输入＄B＄1：＄B＄12；由于两区域均含标志，所以选“标志（L）”；选“置信度（O）”，默认值为95%；选“输出区域（O）”，并置于单元格I1处，选定后的回归分析对话框3见图7.83，按钮，可得回归结果。由于其内容较多，分以下几部分说明。

（4）回归分析结果1见图7.84，此部分用来计算相关系数（Multiple R，在多元回归分析中，为复相关系数）、判定系数（R的平方）、调整后的R的平方、标准误差与观测值个数。

（5）回归分析结果2见图7.85，此部分用来作回归方程的统计检验，分析判断因变量y与自变量x间是否有显著的回归关系。此部分用F检验法，回归方程显著性的原假设是：在总体中，因变量与自变量（多元线性回归是对所有自变量都）不存在线性回归关系。判断回归方程显著性，只要比较F检验的Significance F与显著性水平α的大小。在本例中，6.57407E－07＜α＝0.05，否定原假定，说明所求回归方程有效。

图7.82　回归分析对话框2

（6）回归分析结果3见图7.86，此部分用t检验法，判断回归系数与常数项是否为0，并求其置信区间。原假设为回归系数与常数项为0。判断是否显著，只要比较t检验的P－value与显著性水平α的大小。

本例中，常数项为－2.065，其t检验的P－value为0.03216＜α＝0.05，说明回归方程的常数项不为0；回归系数为1.107，其t检验的P－value为6.6E－05＜α＝0.05，否定回归系数为0的假设，说明自变量与因变量间有线性关系。

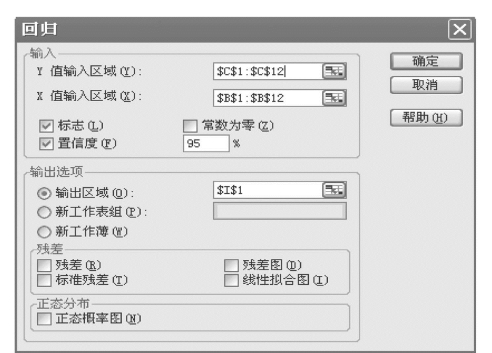
图7.83　回归分析对话框3

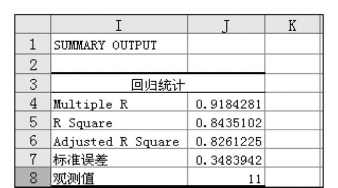
图7.84　回归分析结果1

通过F检验和t检验，所求回归方程Y＝－2.065＋1.017x有效。

以上回归分析的基本方法，同样适用于多元线性回归方程的统计检验。

7.规划求解

流域或区域水资源规划也是水文部门会遇到的业务工作之一，现通过一个实例简要介绍Excel在规划求解中的应用方法。

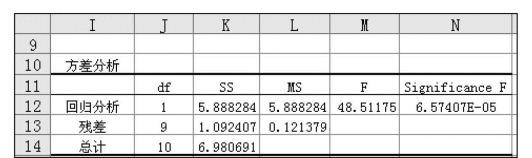
图7.85　回归分析结果2

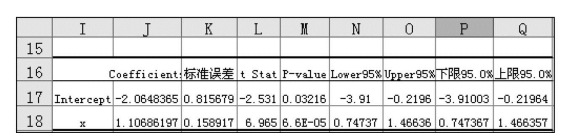
图7.86　回归分析结果3

某水库灌区主要种植小麦、棉花和玉米三种作物（小麦收割后，播种玉米），根据气象和水文预报，下一年来水量为1500万m3，预测小麦、棉花和玉米的毛灌溉定额为120m3/亩，160m3/亩、80m3/亩，三种作物预测产值分别为480元/亩、800元/亩、300元/亩，灌区总面积为10万亩，根据地区种植计划要求，棉花种植面积不得大于4万亩，现需要作明年三种作物面积安排的方案，并求灌区总产值的最大值。

这是一个典型的线性规划问题，设x1、x2、x3分别为小麦、棉花和玉米的种植面积，则这个线性规划问题的数学模型可以写成：

目标函数：　max Z＝480x1＋800x2＋300x3

约束条件：　x2≤4

　　　　　　x1＋x2≤10 x2＋x3≤10

　　　　　　100x1＋160x2＋80x3≤1500

　　　　　　x1，x2，x3≥0

以上线性规划问题可以利用Microsoft Excel的“规划求解”工具很方便地求解。其步骤如下：

（1）按照图7.87规划求解数据的格式将有关数据输入Excel工作表中。其中：

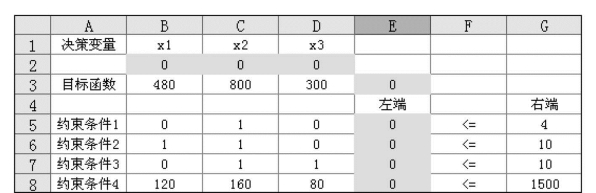
图7.87　规划求解数据

1）单元格B2：D2为决策变量的值（假设初始值为0）。

2）B3：D3为目标函数的价格系数，E3为目标函数值（假设初始值为0），用“＝SUMPRODUCT（＄B＄2：＄D＄2，B3：D3）”计算。

3）B5：D8为约束条件系数，E5：E8为约束条件左端计算结果，其计算与目标函数类似（将单元格E3复制到E5：E8），G5：G8为约束条件的右端项。

（2）在“工具”菜单上，单击“规划求解”，出现图7.88所示的“规划求解参数”对话框。如果“工具”菜单上没有“规划求解”项，则可利用“工具”菜单的“加载宏”功能安装“规划求解”程序，可参阅附录7的安装分析工具库。

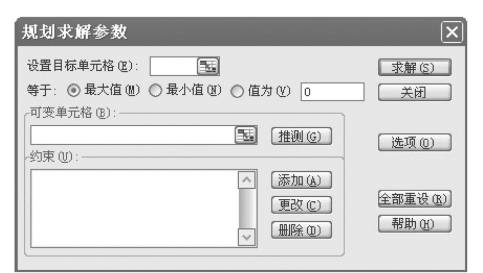
图7.88　规划求解对话框1

（3）对图7.88进行规划求解参数设置：

1）在“设置目标单元格（E）”框中，输入目标单元格的引用或名称E3，然后选择“最大值”。

2）在“可变单元格（B）”框中，输入每个可变单元格的引用或名称（表示决策变量）＄B＄2：＄D＄2。

3）在“约束（U）”框中，按“添加（A）”按钮输入相应的约束条件：

参数设置如图7.89规划求解对话框所示。

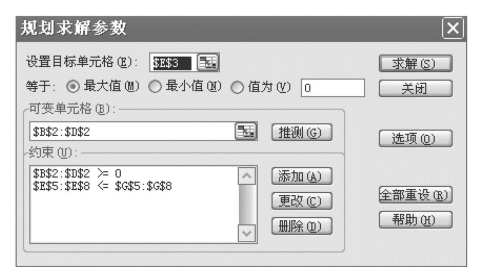
图7.89　规划求解对话框2

（4）对于线性规划，单击“选项”按钮，见图7.90，在对话框中选择“采用线性模型（M）”。

图7.90　规划求解对话框3

（5）单击“求解（S）”按钮，可以得到计算结果，最优解x1＝6、x2＝4、x3＝1.75，总产值Z＝6605，如图7.91所示。

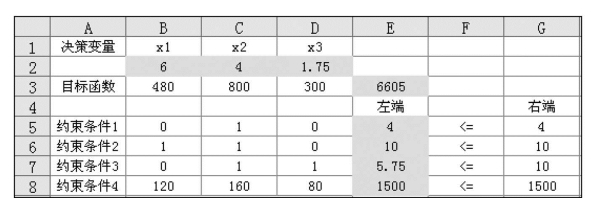
图7.91　规划求解结果

规划求解结果可以保存，还可以选择生成运算结果报告、敏感性分析报告和极限报告。