水文数据处理常用函数

电子表格Excel中有许多函数可供水文数据处理之用，附录6中列出了63种可用于水文数据处理的常用函数名称、功能和格式。

水文数据处理中应用最普遍的函数有均值、求和、极大值和极小值、样本标准差、总体方差、众数、中值、偏态系数等和其他一些统计描述，现分别简介于下。

1.均值AVERAGE（）与AVERAGEA（）

（1）AVERAGE（）。AVERAGE（）函数的功能为计算参数的算术平均数，其格式为：AVERAGE（number1，number2，...）。式中number1，number2，...用于计算平均值的1到30个数值参数，参数可以是数值或包含数值的名称、数组或引用。

（2）AVERAGEA（）。AVERAGEA（）函数的功能为返回所有参数的算术平均值，其格式为：AVERAGEA（value1，value2，...）。式中value1，value2，...表示要求平均值的1到30个参数，其中字符串和FALSE相当于0；TRUE相当于1。参数可以是数值、名称、数组或引用。

例如，要分别计算图7.25 AVERAGE（）和AVERAGEA（）函数的应用中雨量站1和雨量站2在1988年6月6～14日的平均雨量，用上述两个函数计算的结果见图7.25单元格C12：D13。

AVERAGE（）计算所有含数值数据的单元格的平均值；而AVERAGEA（）计算所有非空的单元格的平均值。所以，在图7.25中，用AVERAGE（）计算雨量站1的雨量均值为18.8，而用AVERAGEA（）计算雨量站1的雨量均值为16.7。需要注意的是如果某日雨量单元格内未填入字符而成为空格，则函数AVERAGE（）和AVERAGEA（）不计此单元格。

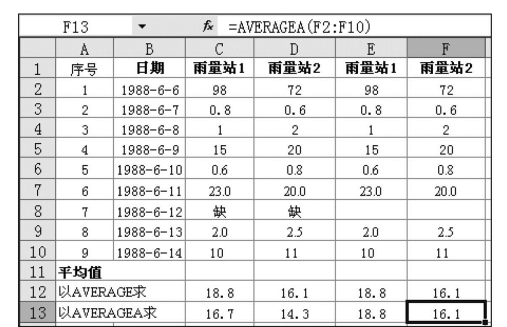
图7.25　AVERAGE（）和AVERAGEA（）函数的应用

2.求和SUM（）及条件求和SUMIF（）

（1）SUM（）。SUM（）函数的功能为计算单元格区域中所有数值的和，其格式为：SUM（number1，number2，...）。式中的number1，number2，...为1到30个待求和的数值。单元格中的逻辑值和文本将被忽略。

（2）SUMIF（）。SUMIF（）函数的功能为计算单元格区域中符合条件部分的和，格式为：SUMIF（range，criteria，sum_range）。式中的range表示要进行条件比较的单元格区域；Criteria则是以数字、表达式或文本形式定义的条件；sum_range是用于求和计算的实际单元格，如果省略，将使用区域中的单元格。

例如，分别统计图7.26中8月份面雨量总量和8月29日～9月3日一次降水过程中流域面平均日雨量大于70的雨量之和。

在G8单元格中求8月份的面雨量之和的公式见图7.26中的编辑栏，表示要在B2：B7单元格区域中计算8月份的面雨量之和。同理，在G9单元格中求面雨量大于70的面雨量和计算公式为：＝SUMIF（G2：G7，"＞70"）。

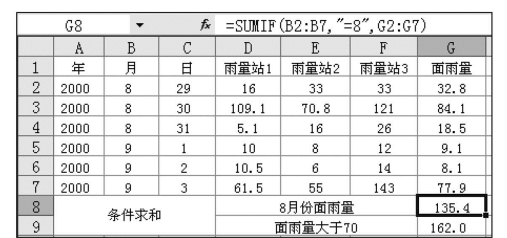
图7.26　SUMIF（）函数的应用

在以上公式中，如省略求和范围，则将计算range中单元格G2：G7的内容。

使用条件求和函数SUMIF（）时，也可以利用“条件求和向导”完成条件求和的任务。

其操作步骤如下：首先执行“工具（T）/加载宏（I）...”命令，加入“条件求和向导”，如图7.27所示。可以利用“工具（T）/向导（W）/条件求和（C）...”，利用“条件求和向导”完成条件求和的公式。加载条件求和向导参照附录7的安装分析工具库。

现仍结合图7.26加以说明。在单元格G8：G9分别推求该次降水过程中8月份面雨量的总和及面雨量大于70的雨量之和。操作步骤如下：

1）执行“工具（T）/向导（W）/条件求和（C）...”，选定计算区域A1：G7，转入图7.28。

2）按钮，转入图7.29。

3）在“求和列（S）”处选择“面雨量”求和，在“条件列（C）”处选择“月”作为求和条件，在“运 算 符（I）”处 选 择“＝”，在“比 较 值（T）”处 选 择“8”，按钮转入图7.30。

4）按钮，转入图7.31。

5）选“只显示公式（C）”，按钮，转入图7.32。

6）用鼠标点击单元格G8，表示将G8单元格用于存放条件求和之结果，按钮，即可在G8单元格得8月份雨量之和，见图7.33。

重新操作一次，在G9单元格中存放面雨量大于70的雨量之和，如图7.34所示。

3.极大值MAX（）与MAXA（）

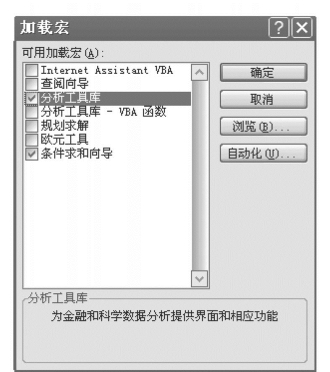
图7.27　加载条件求和向导

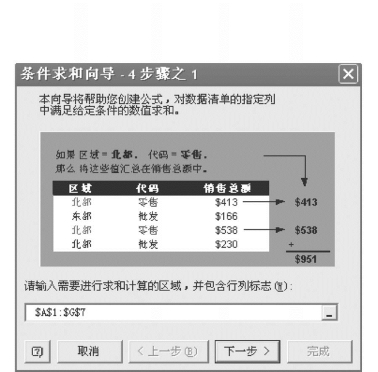
图7.28　条件求和向导示例（1）

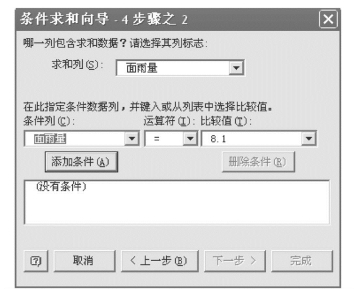
图7.29　条件求和向导示例（2）

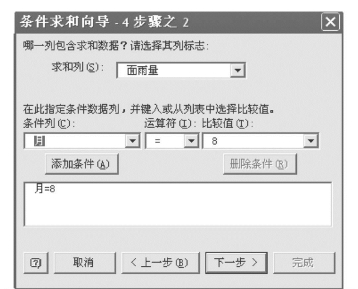
图7.30　条件求和向导示例（3）

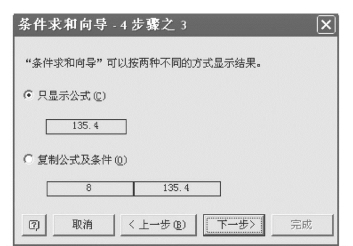
图7.31　条件求和向导示例（4）

图7.32　条件求和向导示例（5）

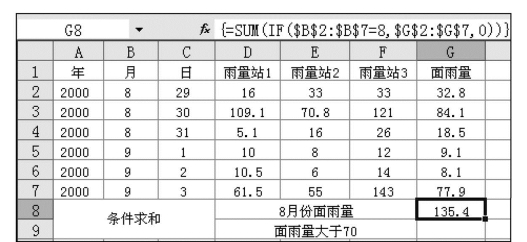
图7.33　条件求和向导示例（6）

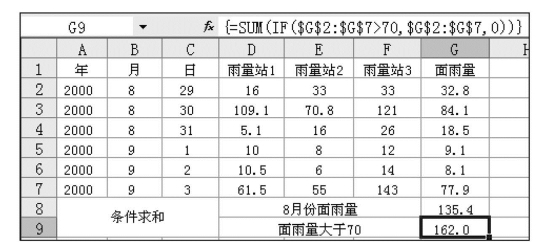
图7.34　条件求和向导示例（7）

（1）MAX（）。最大值MAX（）函数的格式为MAX（number1，number2，...），其功能为返回一组数值中的最大值，忽略逻辑值及文本。式中的number1，number2，...是从中求取最大值的1到30数值、空单元格、逻辑值及文本数值。

（2）MAXA（）。最大值MAXA（）函数的格式为MAXA（value1，value2，...），其功能为返回一组参数中的最大值，不忽略逻辑值及字符串。式中的value1，value2，...是要求最大值的1到30参数，可以是数值、空单元格、逻辑值及文本型数值。

如图7.35所示，单元格C9：C10是分别用MAX（）和MAXA（）函数求某雨量站2000年8月27日～9月2日的最大24小时雨量。

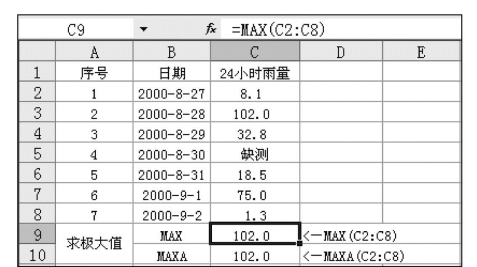
图7.35　MAX（）与MAXA（）函数应用示例1

注意：当处理数据全为负值时，以MAXA（）函数所求的最大值为0。在图7.36中，MAX（）是求所有数值数据的极大值，其结果为－2，而MAXA（）则求所有非空白单元格的极大值（字符串相当于0），故结果为0。

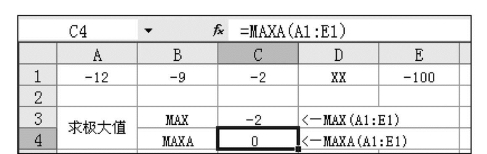
图7.36　MAX（）与MAXA（）函数应用示例2

4.极小值MIN（）与MINA（）

MIN（）与MINA（）函数功能与MAX（）与MAXA（）函数恰好相反。

（1）MIN（）。MIN（）函数的格式为MIN（number1，number2，...），其功能为返回一组数值中的最小值，忽略逻辑值及文本。式中的参数number1，number2，...参见MAX（）函数。

（2）MINA（）。MINA（）函数的格式为MINA（value1，value2，...），其功能为返回一组参数中的最小值，不忽略逻辑值及字符串。式中的参数value1，value2，...参见MAXA（）函数。

注意：当处理数据全为正值且包含拥有字符串的单元格，MINA（）函数所求的最小值为0。在图7.37中，MIN（）是求所有数值数据的极小值，其结果为1.3，而MINA（）则求所有非空白单元格的极小值（字符串相当于0），故结果为0。

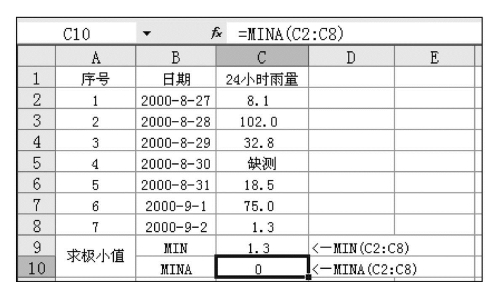
图7.37　MIN（）与MINA（）函数应用示例

5.样本方差VAR（）和VARA（）

样本方差是描述样本统计特性重要的统计参数，用来衡量观测值与平均值间的离散程序，其计算公式为：

式中：n为样本系列容量；xi为样本系列中i序号观测值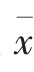；为样本系列的均值。

（1）VAR（）。VAR（）函数计算基于给定样本估算方差，忽略样本中的逻辑值及文本。VAR（）函数的格式为VAR（number1，number2，...），式中的number1，number2，...是总体中抽样样本相应的1到30个数值参数。

（2）VARA（）。VARA（）函数的格式为VARA（value1，value2，...），式中的value1，value2，...是总体抽样样本的1到30个数值参数。VARA（）函数计算基于给定样本（包括逻辑值和字符串）的方差。字符串和逻辑值FALSE为数值0；逻辑值TRUE为数值1。

VARA（）与VAR（）的区别在于VAR（）函数是求所有数值的样本方差；而VARA（）则求所有非空白单元格的样本方差。

在图7.38中，已知某流域雨量站1、雨量站2在1980～1988年的年雨量，其中1986年缺测，单元格L11、M11和单元格L12、M12为分别以公式VAR、VARA计算的方差，而后者因将缺测年份的雨量当成0来计算，故其方差明显增大。

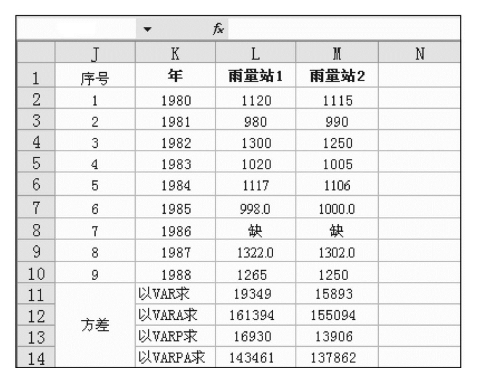
图7.38　VAR（）与VARP（）函数的应用示例

6.总体方差VARP（）与VARPA（）

总体方差是用来衡量观测值与平均值间的离散程度的统计参数，其计算公式为：

（1）VARP（）。VARP（）函数的格式为VARP（number1，number2，...），式中的number1，number2，...是构成样本总体的1到30个数值参数。VARP（）函数的功能是计算基于给定样本总体方差，忽略样本中的逻辑值及文本。

（2）VARPA（）。VARPA（）函数的格式为VARPA（value1，value2，...），式中的value1，value2，...是式中的value1，value2，...是构成样本总体的1到30个数值参数。VARPA（）函数的功能是计算样本（包括逻辑值和字符串）总体的方差。字符串和逻辑值FALSE数值为0；逻辑值TRUE为1。

这两个函数均用来计算总体的方差。但VARP（）是计算所有数值的总体的方差；而VARPA（）则是计算所有非空白单元格的总体方差。

样本方差的计算式（7.1）中的分母为n－1，而总体方差计算式（7.2）中的分母为n，当样本容量n很大时，样本方差将接近于总体方差。图7.38中单元格L13：M14是两种函数计算的结果，可资比较。

7.众数MODE（）

众数是指样本中一组数据或数据区域中出现频率最高的数，其函数格式为：MODE（number1，number2，...），式中的number1，number2，...是用于众数计算1到30个数字、名称或对数值的引用。众数MODE（）的功能是在一组数据或数据区域中出现频率最高的数。如果数据组中不包含重复的数据点，本函数将传回“#N/A”的错误值。

例如在图7.39 MODE（）与MEDIAN（）函数的应用示例中，单元格C2：C8区域中不包含重复数据，故显示“#N/A”。

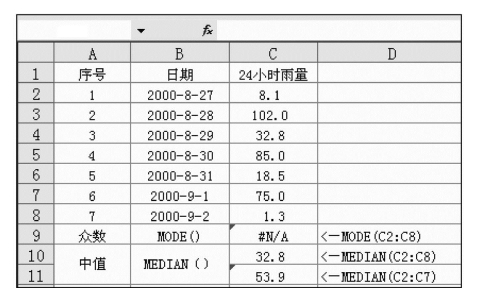
图7.39　MODE（）与MEDIAN（）函数的应用示例

8.中值MEDIAN（）

中值是用来衡量总体的集中趋势统计参数，一个数组或区域数据的中值的定义是，将所有数字依大小顺序排列后，排在最中间的数字，其上与其下的数字各占总数的1/2。如果一组数字的个数为偶数，则将中间两个数的平均值作为中值。

中值MEDIAN（）函数的格式为：MEDIAN（number1，number2，...），式中的number1，number2，...用于中值计算的1到30个数字，名称、数组或者是数值的引用。

例如在图7.39中，单元格C2：C8区域中7个数据从大至小排列，最中间的那个数据为32.8，故MEDIAN（）函数值为32.8。如果去掉最后一个数据1.3，数据个数（6个）为偶数，则本函数值为75.0和32.8的平均值53.9。中值MEDIAN（）函数的功能为依据上述概念推求数组或区域数据的中值。

9.不对称度SKEW（）

SKEW（）函数用来体现某一分布相对其均值为中心的不对称程度，其格式为：SKEW（number1，number2，...），式中的number1，number2，...是要计算不对称度的1到30个参数，可以是数值、名称、数组、或者是数值的引用。SKEW（）函数的功能是计算出样本或总体的不对称度。

不对称度之值有下列3种情况：

（1）SKEW（）＝0，称对称分布。

（2）SKEW（）＞0，称正偏分布，不对称分布的长尾端向正值方向延伸，分布集中在低数值方面。

（3）SKEW（）＜0，称负偏分布，不对称分布的长尾端向负值方向延伸，分布集中在高数值方面。

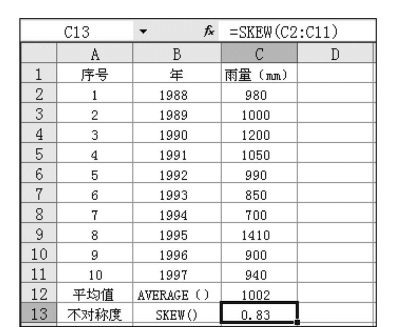
图7.40　SKEW（）函数的应用示例

例如在图7.40中，单元格C2：C11是某雨量站1988～1997年的年雨量，其平均雨量为1002，不对称度为0.83，表明年雨量系列为正偏分布，即年雨量小于多年平均年雨量1002的年份占多数。本例中，年雨量大于多年平均雨量1002有4年，而年雨量小于1000出现6年。

10.分类汇总SUBTOTAL（）

SUBTOTAL（）函数的格式为SUBTOTAL（function　_num，ref1，...），式中的Function_num为数字1到11，以指定分类汇总的函数类别和类别代码（表7.2）；ref1、ref2、...则为1到29个要进行分类汇总的区域或引用。

表7.2　分类汇总的函数类别和类别代码

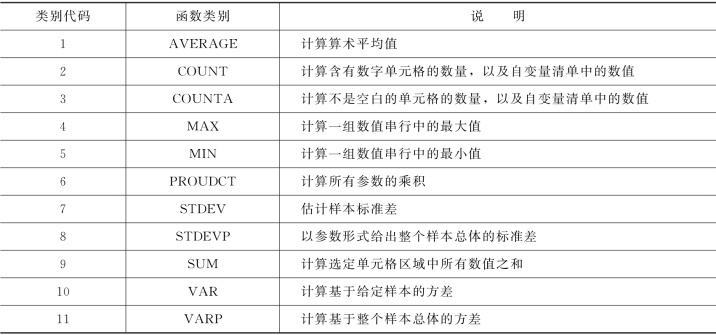
SUBTOTAL（）函数的功能是返回数据列表或数据库的分类汇总，依指定的函数类别，传回几个区域或引用的某一统计量。

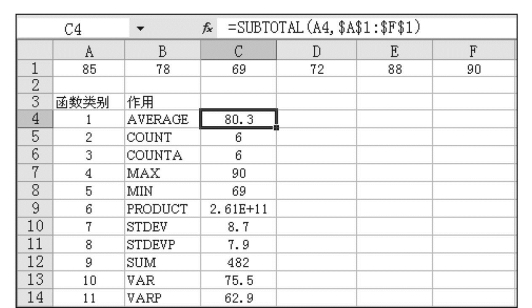
图7.41　分类汇总函数SUBTOTAL（）应用示例(www.xing528.com)

例如，在图7.41中的单元格A1～F1中有6个数据，分别为85、78、69、72、88、90，用分类汇总SUBTOTAL（）函数计算的结果见图7.41中的单元格C4～C14，相应函数类别见B4～B14。

11.相关和回归函数

（1）相关系数CORREL（）。相关分析是水文数据分析中常用的方法，相关系数则是衡量变量之间线性相关密切程度的指标之一。相关系数的计算公式为：

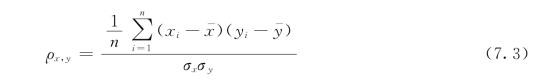
式中：n为数组的元素个数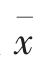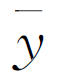；、分别为x和y数组的均值；σx、σy分别为x和y数组的均方差。

CORREL（）函数的格式为：CORREL（array1，array2），式中的array1，array2分别是第一、第二组数值单元格区域。CORREL（）函数的功能是返回两数组值之间的相关系数。当然，两数组区域的数据点必须相同。

相关系数是一个介于－1～＋1的数字，若ρx，y＝0，称为不相关；若ρx，y＞0，称正相关；若ρx，y＜0，则称负相关。

在图7.42中，单元格B2：B13、C2：C13分别为某流域雨量和相应的径流量，在单元格B14输入公式：＝CORREL（B2：B13，C2：C13）后即可算出相关系数为0.92。表示雨量与径流量正相关，其相关关系密切，径流量随雨量的递增而增加。

（2）截距INTERCEPT（）。截距是指线性拟合回归方程的常数项，其格式为：INTERCEPT（known_y’s，known_x’s），式中的known_y’s是因变量数据单元格区域；known_x’s为自变量数据单元格区域。截距INTERCEPT（）函数的功能为返回线性回归拟合线方程的截距。

如图7.42所示的雨量与径流量关系，其回归方程式为：

其常数项即截距为299.87。如果用截距INTERCEPT（）函数推求，则为：＝INTERXEPT（C2：C13，B2：B13）可直接求得，如图7.42中单元格B15所示。

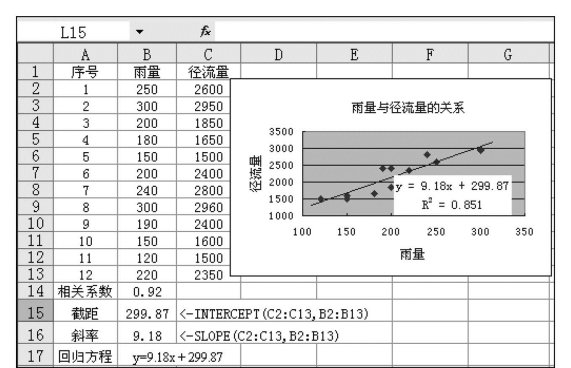
图7.42　相关和回归函数应用示例1

（3）斜率SLOPE（）。斜率是指线性回归方程中自变量的系数，斜率SLOPE（）函数的格式为：SLOPE（known_y’s，known_x’s），式中的known_y’s是因变量数据单元格区域；known_x’s是自变量数据单元格区域。SLOPE（）函数的功能为返回经过给定数据点的线性回归拟合线方程的斜率。

如图7.42中，回归方程式（7.4）中的回归系数值为9.18，亦可用SLOPE（）函数＝SLOPE（C2：C13，B2：B13）直接求得，如图7.42中单元格B16所示。

（4）预测FORECAST（）。预测函数FORECAST（）用已知的因变量数据点与自变量数据点计算其线性回归方程式（但不显示其回归方程），并将其所指定的一组x值代入回归方程式求其y估计值，则可利用FORECAST（）函数，其格式为：FORECAST（known_y’s，known_x’s），式中参数的意义与上述相同。该函数的功能为通过一条线性回归拟合线返回一个预测值。

如图7.43中的雨量与径流量数据，可以利用预测函数FORECAST（）直接求其预测值，其方法如下：首先在D3单元格输入公式：＝FORECAST（B3，＄C＄3：＄C＄14，＄B＄3：＄B＄14），并将其复制到D4：D14。利用回归方程式预测径流量，其结果见单元格E3～E14，可见上述两种方法的结果完全相同。

（5）线性趋势TREND（）。TREND（）函数与FORECAST（）函数作用相同，只不过其输出结果为一组数组，所以在选定区域内输入公式后，按Ctrl＋Shift＋Enter键完成输入。TREND（）函数的格式为：TREND（known_y’s，known_x’s，new_x’s，const），式中的参数known_y’s是满足线性拟合直线y＝mx＋b的一组已知的y值；known_x’s是满足线性拟合直线y＝mx＋b的一组已知的x值，为可选项；New_x’s是一组新x值，希望通过TREND函数推出相应的y值；Const是逻辑值，用以指定是否强制常数为0，如果Const＝TRUE或忽略，b按通常方式计算；如果Const＝FALSE，b强制为0。

本函数的功能为返回一条线性回归拟合线的一组纵坐标值（y值）。

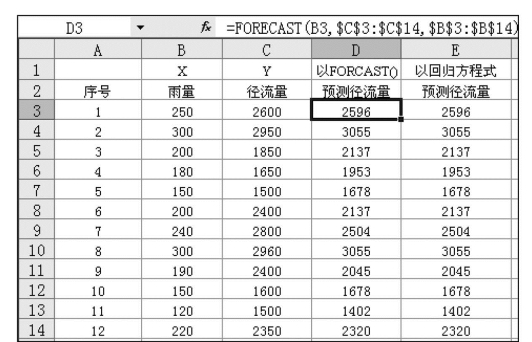
图7.43　相关和回归函数应用示例2

仍以前例图7.42所示的雨量与径流量数据为例，如果直接用TREND（）求预测值，其计算结果如图7.44中的E3：E14所示。它与上述用回归方程计算的结果完全相同。

（6）直线回归函数LINEST（）。直线回归函数LINEST（）的原理是使用最小平方计算最适合于变量区域的回归直线公式，并传回该直线公式的数组。其格式为：LINEST（known_y’s，known_x’s，const，stats），式 中 的 参 数known_y’s，known_x’s，const的意义如前，参数Stats为逻辑值，如果返回附加的回归统计值，返回TRUE；如果返回系数m和常数b，返回FALSE。

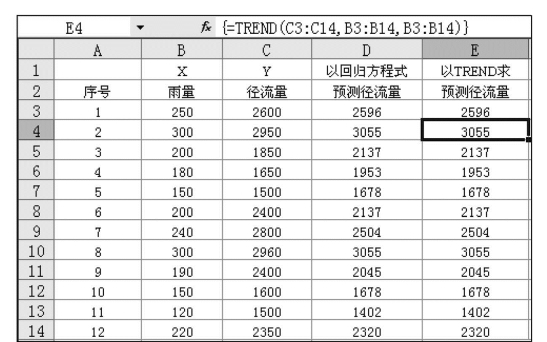
图7.44　相关和回归函数应用示例3

本函数的功能是返回一线性回归方程的参数。由于本函数的返回值为一数组，所以必须在事先选取输出区域内在输入公式后，再用Ctrl＋Shift＋Enter完成输入，才可传回完整的数组公式。

现再以图7.42中雨量与径流量的单一参数数据为例，说明LINEST（）的应用。

1）由于所求对象为单一参数，所以输出的结果为一个5×2的数组，所以选D14：E18作为接受参数的区域。

2）输入公式：＝LINEST（C2：C13，B2：B13，TRUE，TRUE）。

3）按Ctrl＋Shift＋Enter完成输入，获得几组计算结果的数据，如图7.45中D14：E18单元格中所示的数字，它们分别代表图7.46所示的直线回归方程的统计值。根据这些参数，可获得直线回归方程式与判定系统（R2）分别为：

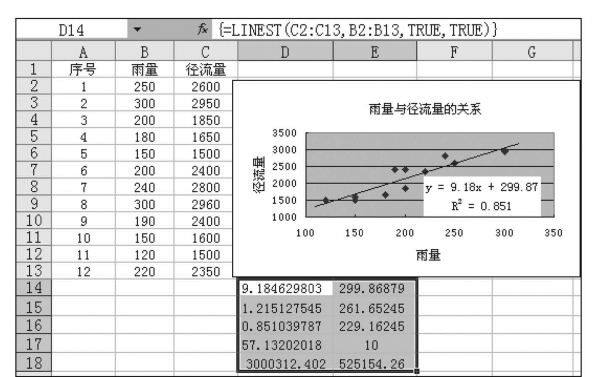
图7.45　相关和回归函数应用示例4

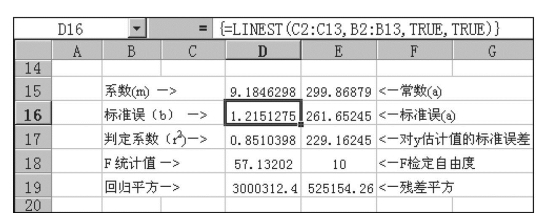
图7.46　相关和回归函数应用示例5

12.描述统计

描述统计可以对一组数据的统计特性进行综合描述，其方法是使用“工具（T）/数据分析（D）”来计算出一组数据的各相关统计值，如“平均值、方差、标准方差、中值、众数、不对称度、峰值、第K个最大值和第K个最小值等。现通过一个具体实例来说明描述统计的应用。

注意：如果在工具菜单栏中没有出现数据分析（D）...，请安装数据分析工具库，见附录7。

某流域1981年5月～1995年5月雨量数据资料，见图7.47中的单元格C2：C16，现应用描述统计对其进行统计分析，其步骤如下：

（1）执行“工具（T）/数据分析（D）...”命令，即出现如图7.48所示的对话框。

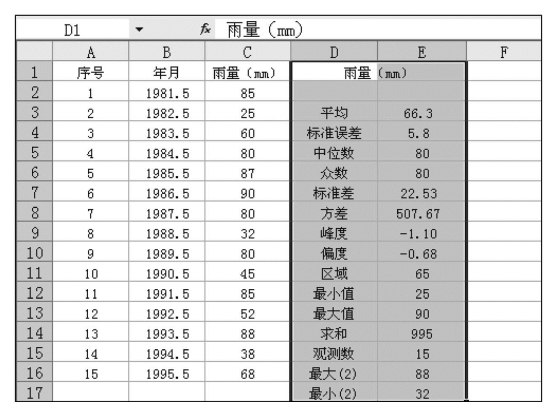
图7.47　数据描述统计示例

图7.48　数据分析对话框

（2）从中选“描述统计”，按Enter键后，出现如图7.49所示的描述统计对话框。

（3）在“输入区域”处，设定要处理的数据区域，本例中选C1：C16。

（4）在“分组方式”中选“逐列”。

（5）选定“标志位于第一行（L）”。

（6）设定输出区域，本例设定数据输出区域为D1。

（7）点选“汇总统计（S）”，设定求第2大的数值和第2小的数值。

（8）按Enter键结束，即可得详细的相关统计数字，见图7.47。

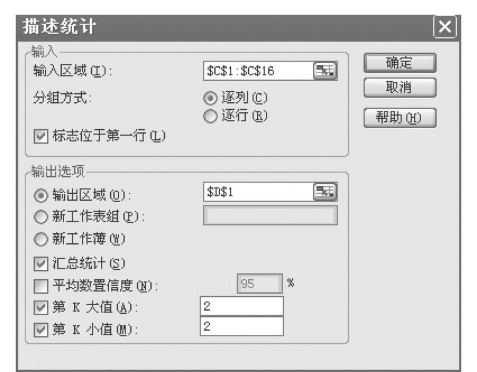
图7.49　描述统计对话框

13.自定义函数

一般而言，Excel的函数应足够满足绝大多数实际问题的应用。若要解决的问题较为复杂，就考虑用撰写VB（Visual Basic）模块的方法来自行建立函数，就是自定义函数。

（1）建立自定义函数。建立自定义函数，得使用“工具（T）/宏（M）/Visual Basic编辑器（V）”，将所需的一串表达式安排在函数内，去进行判断和运算，然后再将表达式的结果传回Excel的工作表中。

自定义函数的格式为：

如图7.50中，C2：C7单元格是某雨量站2000年8月27日～9月1日的24小时雨量，假设要建立一个降雨强度分级的自定义函数，其步骤为：

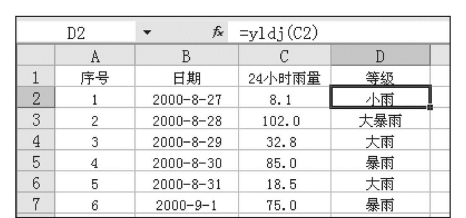
图7.50　建立自定义函数示例1

1）执行“工具（T）/宏（M）/Visual Basic编辑器（V）”命令，转入图7.51。

图7.51　建立自定义函数示例2

2）执行“插入（I）/模块（M）”命令，在图7.51右侧加上一个“代码窗口”的编辑窗口；并于左上角的“工程”窗口内插入一个“模块”数据夹（），其下有一“”，如图7.52所示。

图7.52　建立自定义函数示例3

3）在“代码窗口”的编辑窗口中，输入自定义函数的第一行内容：＝Function Yldj（yl），按下Enter后，将自动补上其配对的陈述式End Function。

4）在Function和End Function内，输入所需的命令内容，如图7.53所示。

5）按工具栏的“视图Microsoft Excel”钮（或按Alt＋F11），可切换回Excel窗口。

6）在图7.50中的工作表的D2单元格中输入自定义函数的表达式：＝Yldj（C2），显示“小雨”，将其复制到D3～D7，就可由自定义函数所安排的运算内容，以24小时降雨量进行降雨强度分级，见图7.50中的单元格D2：D7。

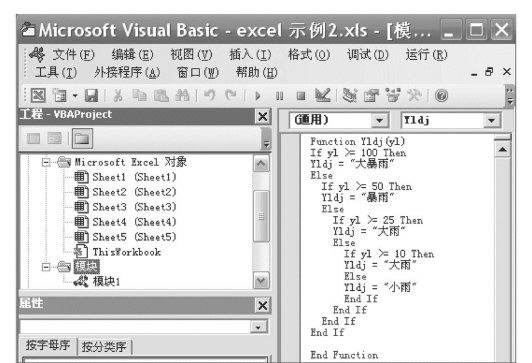
图7.53　建立自定义函数示例4

（2）存盘和重新打开。自定义函数的内容模块，其程序代码的编辑窗口虽独立于原工作的窗口，但其内容仍将随所存在的文件一并储存。故无论在那一个窗口按钮，均可将文件及含有自定义函数内容的模块一并储存。

（3）窗口切换。重新打开文件后，如要重新编辑模块内的自定义函数内容，仍需要再执行“工具（T）/宏（M）/Visual Basic编辑器（V）”命令。

打开程序代码的编辑窗口以后，按工具栏的“视图Microsoft Excel”钮（或按Alt＋F11），可切换回Excel窗口。而按“开始工作栏上的Microsoft Visual...”（或再次执行“工具（T）/宏（M）/Visual Basic编辑器（V）”命令），可切换到模块的代码窗口。

（4）控制简单分支。在自定义函数的处理中，经常会碰到“如果…就…否则就…”等，必须视具体情况，去执行不同分支的操作，有以下3种格式可以采用：

1）格式1：

其功能为当condition条件式成立时，就执行statements处的表达式；否则，就执行elsestatements处的表达式。

2）格式2：

其功能为当condition条件式成立时，就执行statements处的表达式；否则，就执行elsestatements处的表达式。

若情况较为复杂，或为了阅读方便，可将If/End If安排成格式2的区块形式。

3）格式3：

其功能为当condition1条件式成立时，就执行statements1处的表达式；否则，若condition2条件式成立时，就执行statements2处的表达式；否则，再执行elsestatements处的表达式。

由于每个If/End If中还以再加入If/End If，所以就可组合出多层的分支结构情况，如图7.53所示。

（5）分支结构。If/End If结构虽可控制多重分支，但因If/End If需配对使用，故会使得整个自定义函数变得很长，所以最便捷的方式是使用Select Case/End Select分支结构，其格式为：

其功能为：

1）testexpression：为一数值或字符串表达式，通常是安排欲进行比较的参数。

2）expressionlist-n：接于Case后，用以判断分支的条件。其内可为Is比较表达式（如Case Is＜＝2000）；To表达式（如：Case 100 to 200）；还可以是用“，”标开的多组表达式（如：Case Is＜100，Case Is＞＝1000）。

3）statements-n：是当某一分支条件成立时，所执行的一组命令或表达式，其处理范围仅到下一个Case或End Select为止。

Case子句可为多组，其组数并无限制。当所有分支条件均不成立时，才会执行到Case Else到End Select间的elsestatements表达式。

如图7.53中，建立以24小时降雨量进行降雨强度分级的自定义函数，若改用Case Else/End Select来编写，将可缩短程序代码的内容，使程度结构更为明了，如图7.54所示。

Case子句允许多次出现，但其处理顺序是由上而下，依条件选择第一个符合条件的Case进行处理。若有多个Case子句符合条件，则只有最先符合条件的第一个Case子句的表达式会被执行而已。

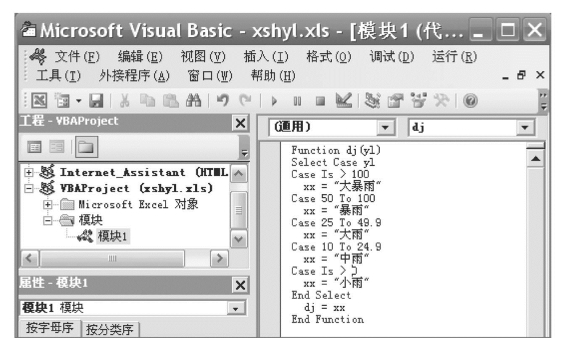
图7.54　建立自定义函数示例5