河流水质模型-水文现代化与水文新技术

在前面建立的一维水质迁移转化基本方程的基础上，进一步对河流水质多组分情况建立模型。在众多水质模型中，以综合反映耗氧有机物的BOD—DO模型最具有普遍意义，是研究较为成熟的水质模型。

6.5.4.1　斯特里特—菲尔普斯（Streeter-Phelps）BOD—DO模型

1.斯特里特—菲尔普斯方程

在稳态条件下，一维河流水质模型的基本方程为：

斯特里特—菲尔普斯建立的BOD—DO模型有以下假定：

（1）方程中的源漏项∑Si，只考虑好氧微生物参与的BOD衰减反应，并认为该反应是符合一级反应动力学的，∑Si＝－K1L。

（2）引起水体中溶解氧DO减少的原因，只是由于BOD降解所引起的，其减少速率与BOD降解速率相同；水体中的复氧速率与氧亏成正比，氧亏是指溶解氧浓度与饱和溶解氧浓度的差值。

由上述两个假设，根据稳态的一维迁移转化基本方程，稳态的一维BOD、DO水质模型可用下列两个方程来表示：

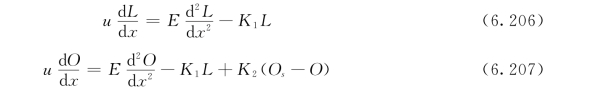
式中：L为x＝x处河水BOD浓度，mg/L；O为x＝x处河水溶解氧的浓度，mg/L；Os为河水在某温度时的饱和溶解氧浓度，mg/L；D为x＝x处河水氧亏浓度，mg/L；x为离排污口处（x＝0）的河水流动距离，m；u为河水平均流速，m/s；K1为BOD的衰减系数，d－1；K2为河水复氧系数，d－1；E为河流离散系数，m2/s。

在L（x＝0）＝L0，O（x＝0）＝O0的初值条件下，求其积分解，得到以下考虑离散和忽略离散时的S—P模型：

考虑离散时：

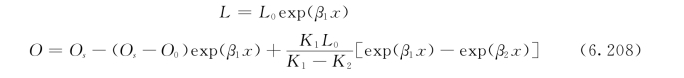
其中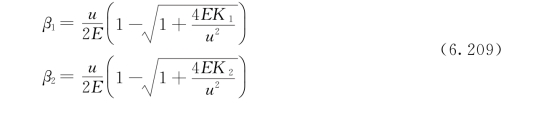　

忽略离散时：

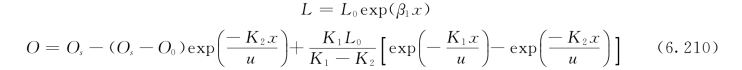
或者用氧亏来描述溶解氧的变化：

2.用斯特里特—菲尔普斯方程推求临界氧亏和临界距离

溶解氧的沿程变化表明了河段内可能出现最大的氧亏值。一般情况下，我们想要知道最大氧亏是多少，它发生在河道的什么位置。假设：xc为最大氧亏发生的距离，称为临界距离，相应的最大氧亏称为临界氧亏D，对应的溶解氧称为临界溶解氧Oc。

（1）临界距离xc。由于临界溶解氧处有，因此，忽略离散项，并令其等于零，有：

由BOD表达式，有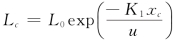，代入式（6.212），得：

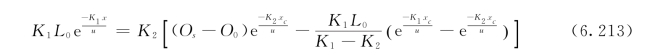
式（6.213）整理后得：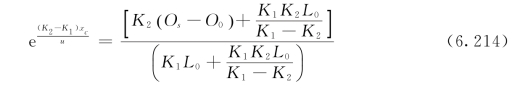

对式（6.214）两边取对数并整理，可求得临界距离xc计算公式：

（2）临界溶解氧Oc和临界氧亏Dc。由K1Lc＝K2（Os－Oc），得：

将临界距离xc计算公式代入，得临界溶解氧Oc计算公式为：

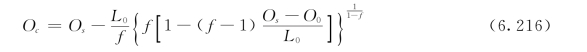
临界氧亏Dc计算公式为：

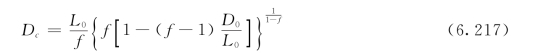
式中：f为自净系数，是复氧系数与耗氧系数之比，即，反映水体中溶解氧自净作用的快慢，是衡量一条河流的环境污染容量的一个指标。T＝20℃下各种水体的f值（Fair，1939）如表6.5所列，可供实用中参考。

表6.5　T＝20℃下各种水体的f值（Fair，1939）

6.5.4.2　托马斯（Thomas）BOD—DO模型

对于一维稳态河流，由于悬浮物的沉淀与上浮也会引起水中BOD的变化。因此，托马斯在斯特里特—菲尔普斯模型的基础上，考虑了一项因悬浮物沉淀与上浮对BOD速率变化的影响，增加了一个沉浮系数K3。其基本方程式为：

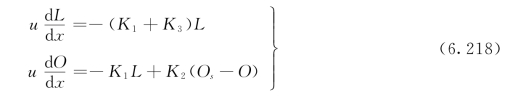
式中：K3为BOD沉浮系数，L/d；其他符号意义同前。

从上式可以看到，托马斯建立的BOD—DO模型在计算溶解氧方程中仍然保留一个K1，这是因为BOD的这一部分减少并不是降解所致，因而与溶解氧的减少无关。

在边界条件为L（x＝0）＝L0，O（x＝0）＝O0的情况下，得到托马斯模型的积分解为：

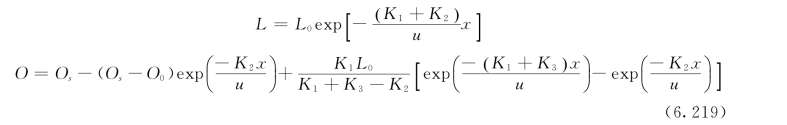
6.5.4.3　多宾斯—坎普（Dobbins-Camp）BOD—DO模型

对一维稳态河流水质方程，在托马斯模型的基础上，进一步考虑由于底泥释放和地表径流所引起的BOD的变化（其变化以速率R表示）；以及藻类光合作用增氧和呼吸作用耗氧以及地表径流引起的DO的变化（其变化速率以P表示）。多宾斯—坎普BOD—DO模型采用以下的基本方程组：

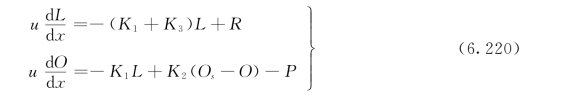
式中：R为底泥释放和地表径流引起的BOD变化率，mg/（L·d）；P为藻类光合、呼吸作用或地表径流所引起的溶解氧变化率，mg/（L·d）；其他符号意义同前。

在L（x＝0）＝L0，O（x＝0）＝O0的边界条件下，得到多宾斯—坎普BOD—DO模型的积分解为：

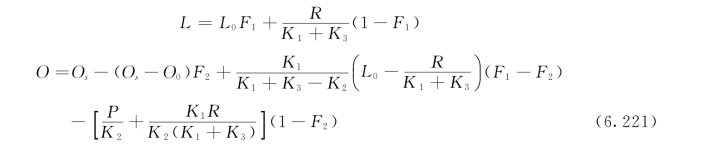
或

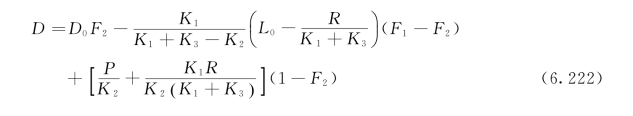
其中

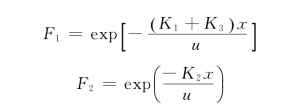
多宾斯—坎普BOD—DO模型中，当参数R、P为零，该模型即为托马斯BOD—DO模型。当参数K3也为零时，该模型即成为斯特里特—菲尔普斯BOD—DO模型。

应用多宾斯—坎普BOD—DO模型同样可求解临界距离xc：

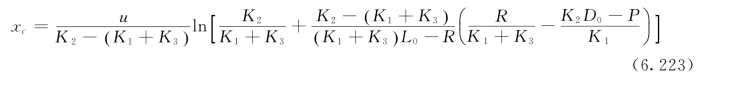
当由给定的临界氧亏Dc，可以推求河段排污口BOD的最大允许排放浓度L0：

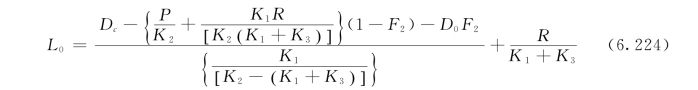
对式（6.223）、式（6.224）采用数值计算方法联立求解，即可同时得到xc和L0。

6.5.4.4　奥康纳（O’Connon）BOD—DO模型

对一维稳态河流，在托马斯模型的基础上，奥康纳将总的BOD分解为碳化耗氧量（LC）和硝化耗氧量（LN）两部分，其方程组为：

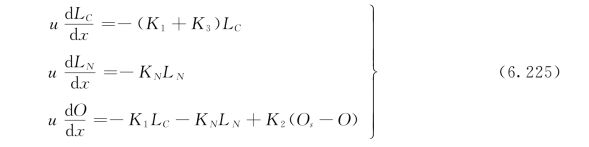
式中：LC为x＝x处河水CBOD浓度，mg/L；LN为x＝x处河水NBOD浓度，mg/L；K1为CBOD的衰减系数，d－1；K2为河水复氧系数，d－1；K3为CBOD的沉浮系数，d－1；KN为NBOD的衰减系数，d－1；其他符号意义同前。

在LC（x＝0）＝LC0，LN（x＝0）＝LN0，O（x＝0）＝O0的边界条件下，可求解得到奥康纳BOD—DO模型的积分解为：

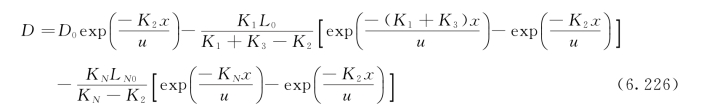
或

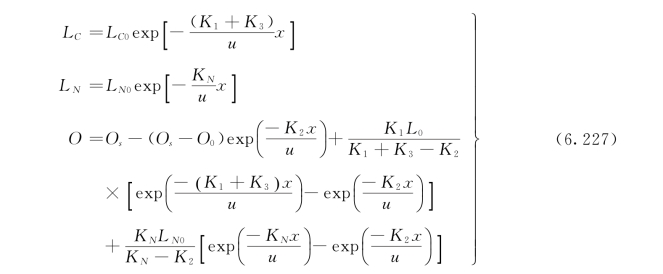
6.5.4.5　一维河流水质的稳态模拟

对于一条实际河流的水质模拟或水质预测，首先必须对研究河段的水量水质基本资料进行收集、整理和分析，其主要工作包括如下几个方面：(www.xing528.com)

（1）河道的计算流量。天然河流的流量变化很大，其流量对河流的自净能力有着重要影响。因此，应根据水质模拟或预测的目的，确定河流的计算流量。在进行水污染控制规划时，由于河道枯水期的流量较小，稀释作用较弱，污染较严重，反映出与河流其他时间更为不利的情况，因此，一般选择枯水期某一设计流量作为计算流量。

（2）河流形态特征资料。包括河道形态，河段各断面面积、平均流速，河床坡度、糙率等。

（3）河流的污染源分布。污染物排放口、取水口位置，污染物的性质与排污量（流量与主要污染物浓度），沿河水质实测资料（COD、BOD5、DO等），以及污水处理现状与规划情况。

（4）河流水质参数。如离散系数E，降解系数K1，复氧系数K2等。

（5）河流支流的上述资料及支流汇入干流的位置。

对于单一河道，根据自身的特点和沿程流量输入与输出的状况，将河道划分成n个计算河段，共n＋1个断面，一维河流水质模拟计算概化如图6.14所示。分段的原则是使得每一河段大体适用一维河流水质模型的应用条件。断面的编号从上游向下游依次为0，1，2，…，i，i＋1，…，n。

图6.14　一维河流水质模拟计算概化图

1.基本关系式

河流上游污染物对于河流下游每一断面水质都会产生影响，而下游的污染物对上游断面的水质影响一般认为可忽略不计。河流每一断面处的水质都可以看成是由上游各个节点与本断面排放的污染物对水质影响的总和，现以BOD5水质为例，用—个线性多项式可以表示为：

式中：ui1，ui2，…，uii为河流中BOD5的传递关系系数；ei0为起始断面的BOD5值L10对第i断面的BOD5值影响的传递系数。

对河流各个节点都可以写出一个类似的多项式：

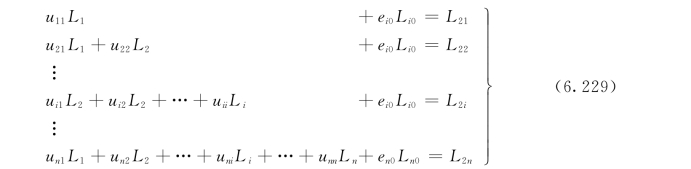
将以上多项式写成矩阵方程，有：

式中U为一个n×n阶的下三角矩阵：

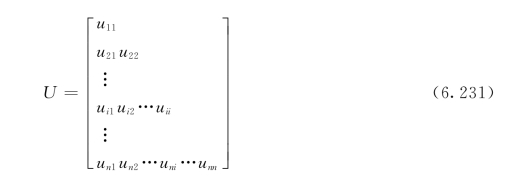
2.BOD5的模拟关系式

按照图6.14中的符号，根据质量守恒原理，可以写出河道各断面的流量Q、水质BOD5和DO的平衡关系式。

流量平衡关系：

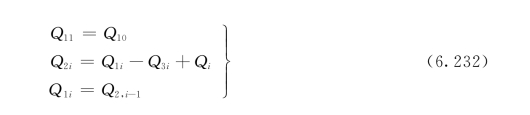
水质平衡关系：

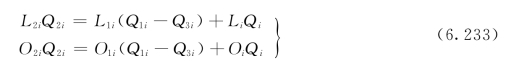
根据斯特里特—菲尔普斯BOD—DO模型，可以写出由i—1断面至i断面之间的BOD5衰减关系与复氧关系：

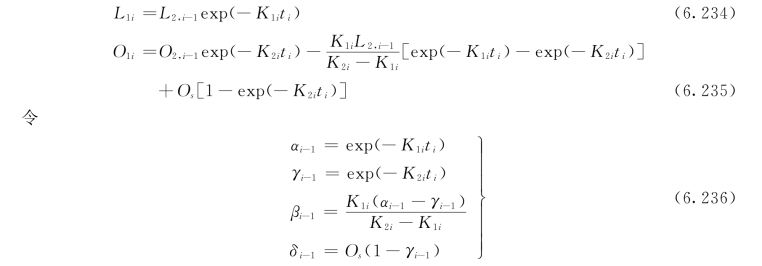
则方程可以写为：

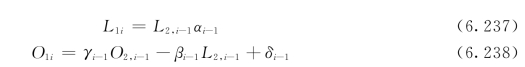
同时由式（6.237）、式（6.238）可以写出：

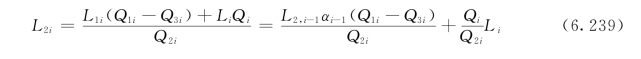
令

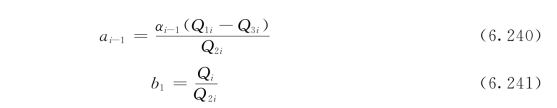
于是可以写出任一断面处的BOD5值与上游各个断面及汇入本断面的污水BOD5值之间的一系列递推关系：

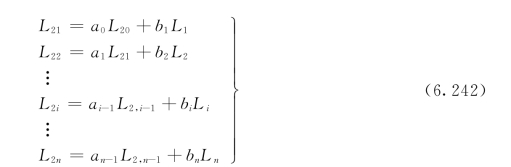
这一递推算式可以用一个矩阵方程表示：

其中：L＝（L1L2…Ln）T；L2＝（L21L22…L2n）T；g＝（g10…0）T，是给出i＝1断面处BOD5值的n维列向量，其中：

g1＝a0L20

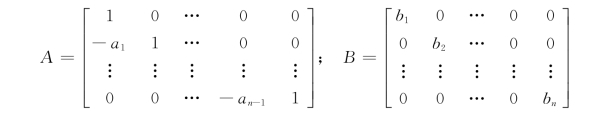
A和B是两个n×n阶矩阵，A非奇异，A的逆矩阵A－1存在，则可以推导出：

矩阵方程给出了河道每一个断面向下游输出BOD5值L2与各个断面输入河流的BOD5值L之间的关系。在水质模拟时，L是一组已知量，L2是待求的模拟量。而在进行水污染控制系统规划时，L2是一组已知的河流BOD5的约束量，而L则是需要确定的量。

3.DO的模拟关系式

据前面所述，有：

令

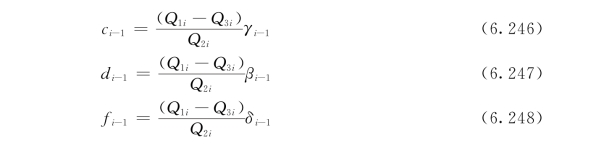
得

与BOD5矩阵方程的推导类似，可以写出上式的一组递推方程，写成矩阵方程形式为：

其中：

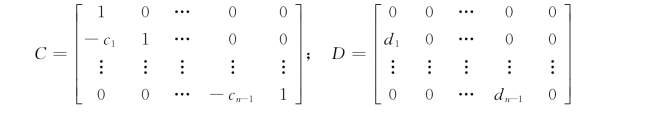
C和D是两个n×n阶矩阵，C非奇异，C的逆矩阵C－1存在，可以推导出：

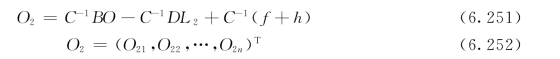
是由河道各断面往下游输出的DO值组成的n维列向量。而

是各断面输入河道的污水的DO浓度组成的n维列向量，通常这是一组已知的量。且

及

都是表征起始条件影响的n维列向量，其中：

整理得：

令

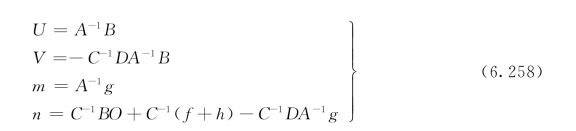
则前面公式分别可写成：

U和V是两个由给定数据计算的n×n阶下三角矩阵，m和n是两个由给定数据计算的n维向量。每输入一组BOD5（L）值，就可以获得一组相应河流的BOD5值和DO值（L2和O2）。由于U和V反映了这种输入、输出的因果变换关系，因而称U为河流BOD稳态响应矩阵，称V为河流DO的稳态响应矩阵。