6.5.3.1 零维水质情况的解析解
对面积小、深度不大、封闭性强的小湖(库),污染物进入该水域后,滞留时间长,加之湖流、风浪等的作用,湖(库)水与污染物可得到比较充分的混合,使整个水体的污染浓度基本均匀。此时,可近似采用零维水质迁移转化基本方程计算和预测湖(库)的污染变化。下面分稳态条件与非稳态条件讨论求解零维水质迁移化基本方程。
1.稳态条件
稳态条件下![]() ,Q=QI,V为常量,源漏项为一阶反应动力学关系(-K1C)时,零维水质迁移化基本方程变为:
,Q=QI,V为常量,源漏项为一阶反应动力学关系(-K1C)时,零维水质迁移化基本方程变为:
Q(CI-C)-VK1C=0
由此得均匀混合水体中污染浓度为:

式中:C为单元均匀混合水体的污染浓度,mg/L;CI为流入该水体的入流污染浓度,mg/L;Q为流入、流出该水体的流量,m3/s;V为该水体的蓄水体积,m3;T为入流水量在该水体容积中的滞留时间,T=V/Q,s;K1为流入该水体的污染物一级反应动力学降解系数,s-1。
2.非稳态条件
这种情况下的零维水质迁移转化方程为:
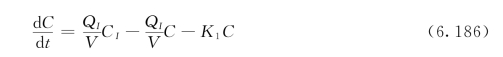
令![]() ,代入式(6.186)得:
,代入式(6.186)得:
![]()
解之得均匀混合的水体中污染浓度随时间的变化为:
![]()
式中:C0、C分别为时间t=0和t=t时的水体污染浓度,mg/L;R为水体的入流量与出流量之比![]()
显然,当R=1.0时,如湖泊的枯水期,入湖流量近似等于出湖流量,式(6.187)则变为:

6.5.3.2 一维河流水质基本方程的解析解
在某些情况下,例如对于河流中的一个均匀河段,当具有足够简单的源漏项和边界条件时,可以用解析方法求解基本方程。
1.稳态解
对于一个均匀河段,如果污染物在河流中只进行一级降解反应,源漏项为∑Si=-K1C,可得下面的一维均匀河段的水质迁移转化基本方程:
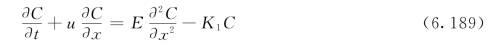
式中:C为河水中t时的污染物浓度,mg/L;u为河段平均流速,m/s;K1为污染物的一级降解系数,s-1;E为纵向离散系数,m2/s;x为沿流程的距离,m。
当![]() 时,即稳定状态,得到如下的常微分方程:
时,即稳定状态,得到如下的常微分方程:
![]()
这是一个典型的一阶常微分方程,当x=0时,C=C0,代入式(6.190),得基本方程的稳态解为:
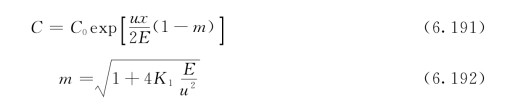
对于一般不受潮汐影响的内陆河流,扩散、离散作用相对于移流作用常常很小,![]() ,排污对上游(x<0)的浓度变化没有影响,此时可直接解得排污引起的下游浓度变化为:
,排污对上游(x<0)的浓度变化没有影响,此时可直接解得排污引起的下游浓度变化为:

上式就是河流水质分析中常用的预测方程。
2.瞬时排污情况的动态解
瞬时突发性向河流排污,是指由于某种特殊原因,如突发性污染事故,在河段的起始断面(x=0)上,把一质量为M的污染物瞬间(t→0)排放于流量为Q的河水中,且污染物也即刻与投放断面的水相混合。混合浓度为![]() ,即t=0时上断面浓度为
,即t=0时上断面浓度为![]() ,以后(t≠0)上断面浓度为零。对于这种情况,可以在初始、边界条件下采用拉普拉斯积分变换法求解得到非稳态的水质方程:
,以后(t≠0)上断面浓度为零。对于这种情况,可以在初始、边界条件下采用拉普拉斯积分变换法求解得到非稳态的水质方程:
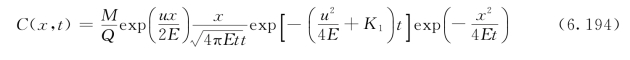
考虑到![]() ,对式(6.194)整理后,得到:
,对式(6.194)整理后,得到:
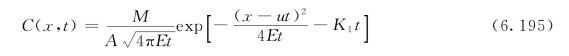 (https://www.xing528.com)
(https://www.xing528.com)
对于难降解污染物,如投入示踪剂,K1=0,式(6.195)可表达为:

该式表示瞬时排放难降解污染物,在不同位置x处所形成的污染物浓度随时间的变化过程。
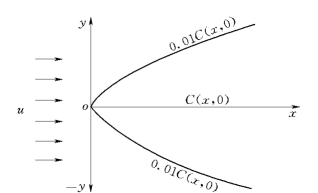
图6.11 无岸边限制的点源扩散示意图
6.5.3.3 平面二维河流水质方程的稳态解
在一个均匀河段的起始断面,从排污口连续稳定地向河流排放污水,由于河流水深相对很浅,近似假定污水排入后即刻在水深方向均匀混合,这种情况下![]() 横向流速v=0,纵向扩、离散输移相对移流输移甚小;E的作用可以忽略,并取∑Si=-K1C,则平面二维河流水质方程变为如下的平面二维稳态水质方程为:
横向流速v=0,纵向扩、离散输移相对移流输移甚小;E的作用可以忽略,并取∑Si=-K1C,则平面二维河流水质方程变为如下的平面二维稳态水质方程为:

式中:C为某点(x,y)处河水的污染浓度,mg/L;x,y分别为河流纵向、横向的坐标,m;u为河流纵向的断面平均流速,m/s;Ey为河流纵向、横向的扩散系数,m2/s;K1为降解系数,s-1。
求解该方程,按水体的边界条件分无边界限制和有边界限制两种情况讨论。
1.无岸边限制的情况
无岸边限制的点源扩散示意如图6.11所示,假定河面很宽,近似于无限,排污口在坐标原点o,离岸边很远,连续稳定地向江中排污,且排入后立刻达到深度上完全混合(称线源)。流速u沿横向均匀分布,故z轴两侧的浓度等值线呈对称情况,仅对上部讨论即可。
设坐标原点处的排污源强度为W,水域的水深为H,x向的流速为u,其他定解条件为:
![]()
在上述条件下,进行拉普拉斯变换,得到解析解:
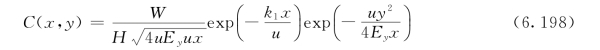
对于难降解物质,K1=0,式(6.198)变为:
![]()
2.有边界限制的情况
实际河流并非无限水域,而是具有两岸和河底。污染物在水流中的扩散将受到边界的限制。污染物扩散到边界后会出现三种可能;一种是被边界全部吸收而粘结在边界上,称全吸收;再一种是遇到固体边界后全部反射回来,称全反射;还有一种是处于二者之间的状态,即部分吸收部分反射。反射情况与边界性质、污染物性质有关。从不利考虑,一般取完全反射进行计算。
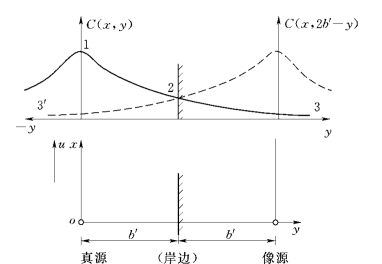
图6.12 单边反射的点源扩散示意图
(1)单边反射。单边反射的点源扩散示意如图6.12所示,水流右边存在岸边限制,水流深度为H,流速为u,在(o,o)处有一污染源(称真源);源强为W。污染物在向下游输移过程中同时向两边扩散。假若无边界限制,W在x断面处沿河宽形成的浓度分布可按无岸边限制情况的公式计算,如图中的实线C(x,y)。但实际上向右边扩散的污染物遇到岸边后则会被反射,并且是全反射。因此,真源在河岸左侧水域形成的污染浓度分布C(x,y),就等于真源和像源在河岸左侧形成的浓度分布相叠加,即:
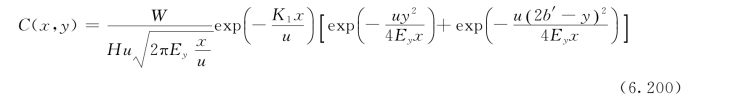
当排污口在岸边时,即岸边排污,b′=0,式(6.200)变为:
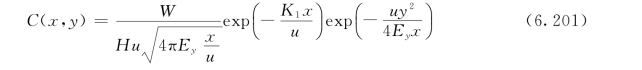
(2)双边反射。双边反射的点源扩散示意如图6.13所示。分中心排污和岸边排污两种情况。
1)中心排污。对于两边都有边界限制和反射,污染源位于河流中心的情况,污染物从污染源向两边扩散,两岸像是两面镜子,因此就有两个像源。由于一个岸边(如右岸)第一次反射的污染浓度遇到对岸(左岸)又产生反射,形成第二次反射,这样逐次反射以至无穷。因而有无数的像源点,把各次反射引起的浓度总加起来,可得:
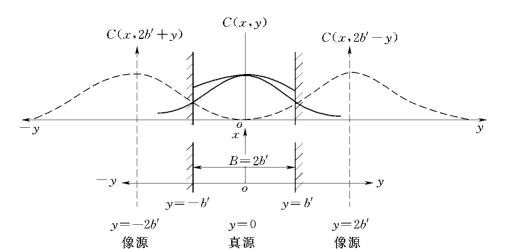
图6.13 双边反射的点源扩散示意图
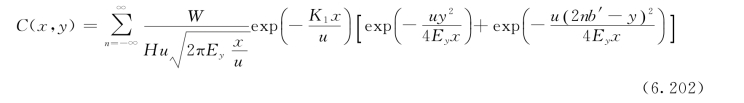
但在实际问题中,如果河流很宽,一般只要考虑一两次反射已足够。
考虑双边一次反射时的二维稳态河流中心点源排污的水质基本方程的解为:
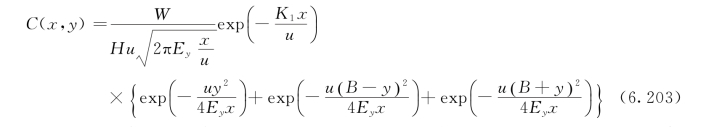
2)岸边排污。当排污口位于岸边x=0,y=0处,河宽为B时,考虑河岸一次反射作用的二维稳态河流岸边排污的水质基本方程的解析解为:
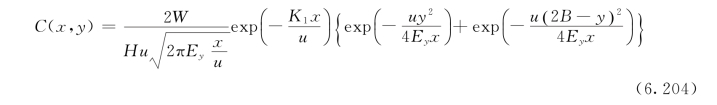
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




