6.3.4.1 人工神经网络(ANN)简介
人工神经网络(简称ANN,是Artificial Nerve Network的缩写),就是采用物理可实现的系统来模仿人脑神经细胞的结构和功能的整体。美国神经学家Hecht Nielsen给出如下定义:神经网络是由多个非常简单的处理单元按某种方式相互连接而形成的计算系统,该系统靠其状态对外部输入信息的动态响应处理信息。ANN是近些年来生物学、认知科学、非线性科学、人工智能、信息处理等学科研究的热点。
由于人工神经网络是对人类大脑结构和功能的一种模仿,使得它具有很多近似人类智能的特点,主要有:
(1)人工神经网络具有并行结构和并行处理特点,即单个神经元功能简单,但大量简单处理单元的集体的、并行的活动能得到预期的识别、计算结果。
(2)人工神经网络具有很强的容错性,即局部或部分神经元损伤后,不影响全局的活动。
(3)人工神经网络的信息是分布存储的,即有记忆的信息存储在神经元之间的权中,从单个权中看不出其存储信息的内容。
(4)人工神经网络具有很强的自适应性,即可通过对样本的训练学习,来确定网络的连接权和阈值。
(5)人工神经网络是一个大型非线性动力系统,可以充分考虑系统的非线性特性。
人工神经网络模型和算法种类很多,现主要介绍一种非线性变换单元组成的前馈网络,简称B—P网络,它是目前众多的ANN模型中应用最为广泛的模型之一。B—P网络结构如图6.1所示。
B—P网络包括输入层、输出层、一个或多个隐含层,每层含有多个神经元。各层之间以权值相连,每个神经元的初值定义为阈值。
B—P网络的变换为一个非线性函数,即输入与输出满足非线性单调上升,输入、输出非线性函数如图6.2所示,对于多层的网络,这种f(u)函数所划分的区域不是线性划分,而是由一个非线性超平面组成的区域,它是比较柔和、光滑的任意界面,因而它的分类比线性划分精确、合理,这种网络的容错性好。
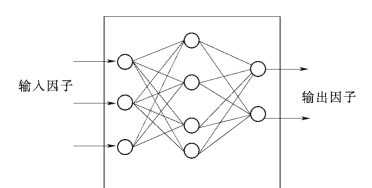
图6.1 B—P网络结构图
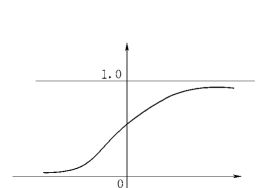
图6.2 输入、输出非线性函数
B—P网络的数学表达式为:(https://www.xing528.com)
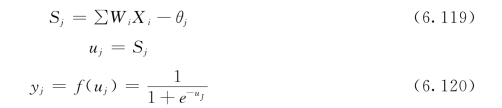
B—P网络是完成n维空间向量对m维空间的近似映照,这种映照是通过神经元之间的连接权和阈值来实现的。B—P网络的“智能”来自于“学习”或“训练”,学习过程分为两个阶段,即信息的前向传播过程和误差的反向学习过程。信息的前向传播过程是指外部输入的信息经输入层、隐含层的神经元逐层处理,向前传播到输出层,输出结果。误差的反向学习过程则是指如果输出层的输出值与样本的期望值有误差,则该误差沿原来的连接通路反向传播,通过修改各层神经元的权值和阈值,使得误差变小,经反复优化,当误差值小于允许误差值时,网络的训练过程即可结束。
6.3.4.2 ANN与水文系统的联系
可以看出,ANN的上述特点与水文系统方法有着密切的联系。水文系统识别就是利用观测数据和先验知识,建立系统的数学模型,估计参数,从而掌握客观水文规律,预报未来径流的大小。ANN的典型应用之一就是让系统本身通过大量学习来掌握非常复杂和细致的各种合乎规律的技巧。因此,ANN可以应用于水文系统。
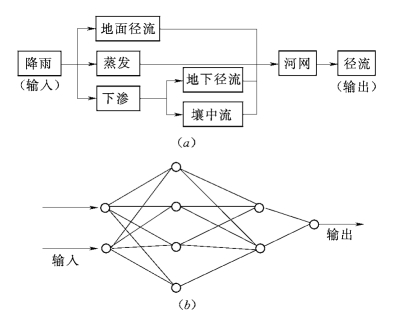
图6.3 水文系统与人工神经网络结构图
(a)水文系统;(b)前馈型人工神经网络模型
特别是水文系统与ANN具有相同结构。以降雨—径流为例,水文系统以降雨为输入,径流为输出,从降雨到径流,中间要经过复杂的过程,其中包括蒸发、下渗、产流、汇流等环节,受到地形、地貌、下垫面因子、土壤地质以及人类活动等多种因素的影响,水文系统是一个非线性系统。水文系统与人工神经网络结构如图6.3所示,水文系统结构如图6.3(a)所示。各个环节或者并行排列,或者串联排列,形成一个相互制约、相互联结的网络结构。而人工神经网络就是一个大型非线性动力系统。各神经元或者分层排列,或者互相联结,或者每个神经元和周围的神经元相联。并因其联结方式的不同形成不同的网络结构,如前馈网络(B—P网络),反馈内层互联网络,反馈型局部联结网络等。其中,以前馈型人工神经网络模型与水文系统结构最为相似,如图6.3(b)所示。B—P网络采用线性阈值硬变换或单调上升的非线性变换来反映输入输出的关系。由此可见,ANN完全可以用于解决非线性水文系统的识别问题。
在解决问题的思维方式方面,人工神经网络模型与水文系统也是一致的,都是把对象放在系统中加以考察,着眼于从整体与部分(要素)之间、整体与外部环境之间的相互联系、相互制约、相互作用的关系中综合他、精确地考察对象,以达到最佳处理问题的一种方法。
6.3.4.3 B—P网络结构的数学表达
多层B—P网络结构如图6.4所示。
B—P网络包括输入层、输出层、一个或多个隐层,每层含有多个神经元。各层之间以权值相连,每个神经元的初值定义为阈值θ。B—P网络的数学模型可表示为:
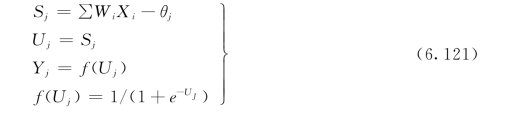
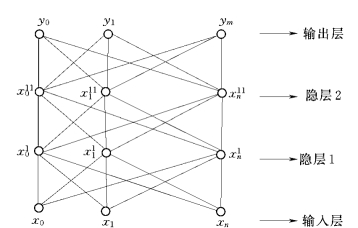
图6.4 多层B—P网络结构图
B—P网络是完成n维空间向量对m维空间的近似映照,这种映照通过各种神经元之间的连接权和阈值来实现。对P个近似映照(x1,y1,…,xp,yp)进行训练学习,其目的就是得到神经元之间的连接权W和阈值θ。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




