星载调零天线原理-航天器天线设计技术

星载自适应调零天线根据调零过程中是否需要反馈，可分为两大类：闭环调零天线（见图6-37中的反馈回路）和开环调零天线。闭环调零天线需要反馈回路，而开环调零天线不需要。图6-37中天馈子系统接收的信号包含有用信号、干扰信号和噪声，经过射频通道加权合成后送往转发器。调零天线根据接收到的信号决定是否启动调零，通过某种调零算法生成调零权值，置入波束形成网络，在干扰信号方向形成零点，从而对干扰进行有效抑制。

图6-37　调零天线原理框图

1.闭环调零天线

闭环调零天线使用迭代算法，根据合成功率反馈、前次权值和方向图变化等信息更新权值，最终在干扰方向形成零陷。闭环调零天线最早为1965年Howells提出的自适应旁瓣对消技术，Applebaum针对该类天线提出了自适应干扰对消算法，取名为Howells-Applebaum算法，属于最陡下降/梯度搜索算法。1974年Reed等人提出了直接采样矩阵求逆算法（Sample Matrix Inversion，SMI）。

由于梯度法硬件、软件实现简单，因此调零天线多采用该算法及其变种算法。以下介绍一种保形梯度算法。

首先给出梯度法形式：

其中，是代价函数的梯度，ε2与权向量w（n）有关，步长因子μ可以是一个标量或者矩阵。目标是使代价函数的梯度最小化，代价函数如下所示：

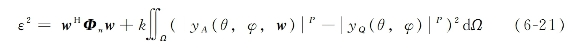
其中，w为自适应权值；yA（θ，φ，w）为自适应方向图；yQ（θ，φ）为静态方向图；Φn为协方差矩阵（干扰+噪声）；k为调零参数（k值较大时对方向图保形较好而调零不会很深）；P为调零参数（不同的P值对应不同的应用场景）；Ω为覆盖区域。

代价函数的第一部分是利用梯度法降低干扰电平，第二部分是方向图幅度差异，用来使两个方向图在覆盖区域尽可能一致，从而在有效减小干扰的同时进行方向图保形。

2.开环调零天线

开环调零天线使用空间谱/波达角估计（DOA）技术与调零算法相结合，首先对干扰方向进行判定，然后在该方向置零点，因此该类调零天线无须迭代。

空间谱估计技术可以得到比天线波束宽度小很多的空间分辨率，因而称为超分辨算法。1969年Capon使用功率最大似然估计方法来求解天线阵的最小方差无失真响应，通过搜索功率谱得到波达角，在得到波达角的同时也得到了调零权值。1979年Reddi提出了最小范数法，通过求解优化问题优化权值向量，使权值向量与信号特征向量子空间正交，通过搜索伪谱得到波达角。1986年Schmidt提出了多重信号分类（MUSIC）算法，利用噪声子空间和信号子空间的正交性，通过搜索伪谱得到波达角。1989年Roy和Kailath提出了通过旋转不变性技术估计信号参数（ESPRIT），利用信号子空间的旋转不变性，其中信号子空间由两个具有平移不变性结构的天线产生。

由于MUSIC算法对阵列流形要求不苛刻，只要预先确定阵列几何结构即可，同时又具备很高的分辨率，因此被科研工作者广为研究，成为最为流行的空间谱估计算法。以下主要对该算法进行介绍。

（1）MUSIC空间谱估计

MUSIC算法利用阵列的几何结构进行空间谱估计，可以对入射信号数量、波达角和信号强度做出无偏估计。该算法对阵列结构的依赖性很高，必须预先准确知道阵列结构，因此实际使用过程中需要进行阵列校准。

MUSIC算法假设每个信道中的噪声是不相关的，因此噪声的相关矩阵是对角矩阵；入射信号有可能相关，所以信号相关矩阵不是对角矩阵。当信号强相关时，传统MUSIC算法可能会失效，所以需要用其他算法补偿。

在窄带信号的前提下，若有D个信号入射到M元阵列天线上，则第M个阵元接收的信号为：

写成矩阵形式为：

其中，s（t）=［s1（t），s2（t），…，sM（t）］T为入射信号矢量，A（θ）为阵列流形，a（θi）为第i个信号对应的阵列导向矢量，n（t）=［n1（t），n2（t），…，nM（t）］T为噪声矢量。

MUSIC算法需要满足下列前提条件：

1）阵元数量大于信号数量M＞D，并且不同阵列导向矢量线性独立。

2）噪声不相关。

3）信号非强相关。

4）噪声与信号不相关。

由以上前提，可以得到阵元接收信号的自相关矩阵：(www.xing528.com)

对接收信号自相关矩阵Rxx进行特征分解，可以得到：

其中，Us为M×D矩阵，D个大特征值对应的特征向量张成的信号子空间；Λs为D×D对角阵，对角元素为D个大特征值；Un为M×（M-D）矩阵，（M-D）个小特征值对应的特征向量张成的噪声子空间；Λn为（M-D）×（M-D）对角阵，对角元素为（M-D）个小特征值，等于。

理论上，噪声对应的（M-D）个特征值等于零，但由于实际中都是使用有限个采样样本生成自相关矩阵，因此对应于噪声的特征值并不等于零，也并不相等，而是一组比较接近的很小的数值。随着样本数的增加，噪声方差逐渐减小，这些小特征值将会是一组很接近的数。因此通过确定小特征值的数量K，可以确定出信号的数量D（等于M-K）。

特征值λi和特征向量ui满足：

由于Rnn表征噪声方差，因此对于（M-D）个小特征值和小特征向量，有：

由于矩阵A是满秩矩阵，矩阵Rss为非奇异的，因此有：

上式表明，阵列流形A（θ）中每一个来波信号方向对应的导向矢量ai（θi）与噪声子空间Un正交，而其他方向对应的导向矢量与噪声子空间非正交。利用该特性，即可实现DOA估计。

根据以上分析，利用来波信号导向矢量与噪声子空间的正交性，对全空间进行遍历，零值点即为来波方向。由于实际中信号采样样本数有限，再加上噪声的影响，所以来波信号方向导向矢量与噪声子空间不能完全正交，只能使用搜索最小值来代替零点。于是得到DOA估计公式：

而在使用过程中，可以通过搜索MUSIC空间谱（伪谱）的峰值进行DOA估计：

或者

将上式中θ替换为（θ，φ），即可将其扩展到面阵或者多波束天线。

（2）调零权值计算

根据空间谱估计技术得到波达角结果，使用保形调零算法即可在波达方向形成方向图零点。

由于调零天线的零点不是陡降的，因此调零后可能会减小通信区域。为了提高调零后可通信区域的比率，需要在有效抑制干扰的前提下，使调零方向图与原静态方向图尽量接近，即对主波束进行保形。整个问题即求解如下约束优化：

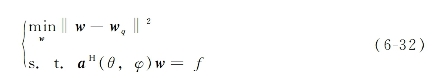
其中，aH（θ，φ）为干扰方向对应的导向矢量，f为约束条件，当f=0时，即为求解最优调零权值问题，wq为正常工作（不调零）时的波束静态权值，w为调零权值。通过拉格朗日算子可以求解上述约束调零权值最优化问题，得到最优权值为：

由上式，最优权可被看作静态权减去其在约束子空间的投影向量，即静态权在约束子空间的正交补空间的投影向量。由于调零权值的生成与干扰方向对应的导向矢量密切相关，因此，干扰信号的DOA结果直接影响到调零效果。

3.两类调零天线对比

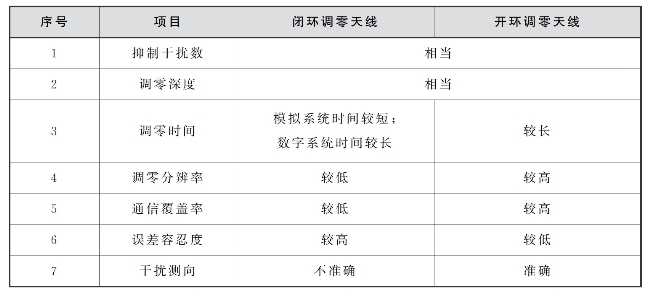
两类调零天线各有其优缺点。目前，军用通信系统多工作于Ku频段以上，且工作带宽最少为几百兆赫兹。受限于数字器件水平，尤其是A/D采样速率，使用数字采集系统的调零天线由于需要多次采集才能收集到整个工作频段内的干扰信息，所以调零时间相对较长。闭环调零天线采用迭代算法，通过多次迭代直接得到方向图零点，而开环调零天线先检测干扰方向，然后在该方向设置方向图零点，所以开环调零天线调零效果和保形效果均优于闭环调零天线。但是开环调零天线干扰检测完全依赖于天线阵列结构，因此对误差的容忍度较低。两类调零天线对比如表6-5所示。

表6-5　两类调零天线性能对比