选用物理光学（PO）理论来计算反射面天线的远场（参见附件A2），从而实现对其性能的精确分析与控制。
目前有很多种算法可以实现对赋形反射面天线的优化设计，在众多的算法中，Minimax算法在实际工程应用中最为实用。因为该算法可以根据实际需要灵活地设置目标函数。如果设计参数合适，优化结果能够保证即使在性能最差的评估点也能满足设计要求。
历史上，第一个极小极大值（Minimax）问题是由法国数学家Jame Waldegrave在1713年研究一个二人纸牌博弈时提出的，只不过作者当时并未用到极小极大值这个术语。由于目标函数的特殊性，近些年来随着计算机技术的发展，极小极大值算法在工程设计、电子线路规划、对策论、博弈论等领域中有着广泛的应用，备受关注。
在赋形反射面优化设计中，极小极大值问题的具体数学模型如式（6-8）所示：
其中，x=（x1，x2，…，xI）T∈RI是一个含有I个元素的向量，由表征反射面形状的参数所构成；fj（x）是关于x的函数，j=1，2，…，J，其中J表示在服务区所选取的观测点数目，fj（x）表示在第j个观测点计算所得的天线性能与设计指标之间的差异，其具体表达式如式（6-9）所示：
其中，Dj是第j个观测点设计指标要求，Gj是设计参量为x的情况下第j个观测点的计算结果，wj是权重系数。(www.xing528.com)
表达式
的含义为：变量x确定为某一特定值时，函数F（x）的值是J个函数fj（x）（j=1，2，…，J）之中的最大值。如果j=M，那么此时第M个观测点的增益与设计指标要求之间的差距最大。优化所要做的就是在x的某个限定范围X内，寻找函数F（x）的最小值。也就是说通过调节优化变量x，提高第M个观测站的增益，缩小其与设计指标之间的差异，最后使F（x）趋近于零。
以覆盖美国版图为例，采用赋形反射面天线技术，通过优化单馈源照射下反射面的形面展开系数，得到美国地图形状的方向图。期望方向图如图6-11所示，优化得到的等高线方向图如图6-12所示，反射面表面形状相对于标准的抛物面的变形量如图6-13所示。
图6-11 期望方向图（图中等高线数值的单位为dBi）
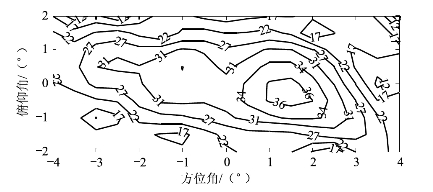
图6-12 优化得到的美国版图形状等高线方向图（图中等高线数值的单位为dBi）
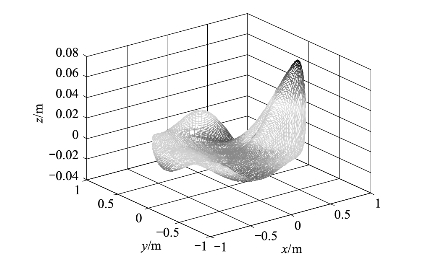
图6-13 反射面的表面变形量
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
