航天器天线设计技术：赋形反射面的方法

反射面的赋形通常是以一个标准抛物面为参考进行的，通过改变反射面任意部分的形面来达到对天线辐射场幅度和相位的再分配而形成赋形波束。由于实际赋形反射面是一个连续较平滑的反射面，因此相对于理想抛物面的变形形面一般要求连续且二次可导。因此，赋形反射面通常表示为一个基础形面和一个变形曲面的合成反射面。其中，基础形面通常为抛物面，根据需求也可以使用双曲面或椭球面，甚至一个已经赋形形面都可以作为参考反射器表面，在该表面的基础上进行赋形；变形曲面即形面变形的曲面，为了保证其连续且可导，通常由一组正交基函数来表示。目前表示反射面变形形面的两种较为通用的基函数是Zernike多项式和B-Spline多项式。

（1）Zernike多项式

Zernike多项式展开式是描述发生适度形变的赋形反射面天线表面的一种十分有效的方式。Zernike多项式是一个复数函数，但是在描述反射面天线表面时，只用实数部分就可以了。用Zernike多项式表示反射面的形式如下：

其中，是幅度系数，是反射面的参考方向值，t和φ是反射面在口径投影坐标系下的参数，（t）是关于位置的Zernike多项式函数，包括tm，tm+2，…，tn等项数。

（t）的定义及Zernike多项式的正交性为：

Zernike多项式在单位圆内是正交的，因此在实际应用中需要把反射器真实口径投影在单位圆内进行计算，同时考虑到该多项式在圆边缘可能存在变化量较大情况，因此实际反射器口径在投影至单位圆时其范围要小于1。由于Zernike多项式每一种模式都对应一个关于整个单位圆的形变（图6-9），因此式（6-2）表示反射面变形形面是m×n种关于单位圆变形的加权和，可通过幅度系数进行调整；同时该特性也说明由Zernike表示的反射面形面是一种全局的表征方法，任何一项系数的变化都会带来整个形面的变化，由该多项式优化得到的形面也比较光滑；m、n数值与反射面大小无关，仅表示反射面赋形能力，m、n数值大可以提供形面变形的模式就多，反射面赋形的能力就强，反射面变形也就剧烈。此外，由Zernike多项式的特点可知，当m=0，n为偶数的情况下，每一种模式都表示一种旋转对称结构下的形面，因此当反射面需要旋转对称结构的变形要求时，通过对m和n参数的限制即可实现其变形控制。

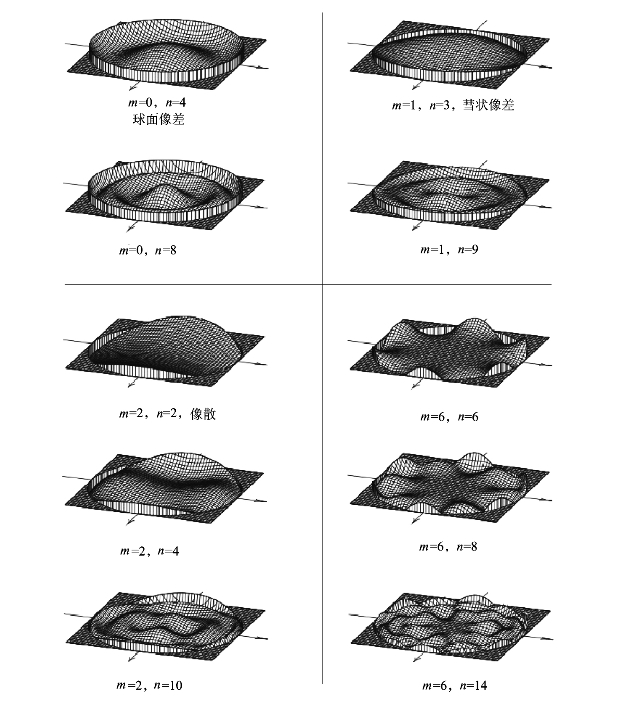
图6-9　表征反射器形面变形的Zernike模式示例

（2）B样条基函数

当用B样条基函数B-Spline多项式表示反射面时，反射面的表面方程如下：

其中，cij是样条函数的系数，Bij是B样条多项式，每个样条函数都只在反射面天线的某一部分是非零的，组合起来构成一个有效的整体反射面：(www.xing528.com)

其中，Bi是一个三次样条多项式，它与一系列所谓的节点有关。t1，t2，…，tM这M个点构成一个序列，即-∞＜t1＜t2＜…＜tM＜∞，则Bi在这些点构成的（M-1）个间隔内是一个连续的三阶多项式，并且在每个节点处关于x有连续的一阶和二阶导数。三次样条多项式具有以下三条特性：

（1）编号为k的三次样条多项式Bk（x）由tk-2，tk-1，tk，tk+1，tk+2五个点唯一确定。

（2）x≤tk-2或者x≥tk+2时，Bk（x）=0。

（3）在tk-2≤x≤tk+2区间内，Bk（x）＞0。

三次样条多项式的具体定义如下：

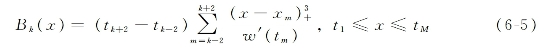
其中，

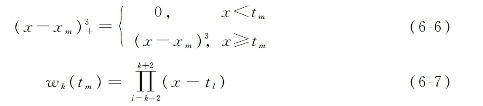
与Zernike多项式不同，三次B样条反射面基函数的每一项仅代表其所在位置附近5个点上（除边界）的变形，其他范围与该点无关，如图6-10所示。整个反射面的形变密度由m、n数目来确定，m和n数目越多，反射面被划分的网格越密，反射面赋形的形变单位也越小，反射面的变形越剧烈，m、n两个方向上网格划分密度可以不同，由B样条表征的反射面形面是一种局域的表征方法，因此相对Zernike系数其赋形形变更加剧烈。

综上，反射器的赋形形面可以由全域基Zernike函数和局域基B样条函数分别表示，对于不同类型的变形形面可以选用不同函数来表达。相对波长较小的口径赋形能力较弱，基函数系数选择较小，相对波长较大的口径赋形能力较强，基函数系数选择较大。由两种多项式表示的基函数可以覆盖大多数情况，对于有特殊要求的赋形反射器，例如需要节点控制形面的网状反射面，则需要用特殊基函数进行表达。

图6-10　单位基函数的示例