1.有限元计算原理
有限元分析法是以结构力学和弹性力学为理论基础，以有限单元为计算主体，对复杂结构工程进行数值计算的方法。其核心思想是将实际结构划分为有限个离散的简单单元的组合体，实际结构的物理力学性能可以通过对这些离散单元进行分析，并对计算结果进行整理得出满足工程精度的近似结果，从而替代对实际结构的分析。
有限元分析法的基本思路是将一个连续的整体分割成有限多个互不重叠且按一定方式相互连接的单元，通常利用单元内各个节点的数值和插值函数来近似表示每个单元的场函数，再利用在每个单元内假设的近似函数来分片表示全部求解域上待求的未知场函数。根据连续性条件联立方程组，并采用插值函数计算各单元内场函数近似值，从而得到全部求解域上的近似解。
合理选择网格的疏密程度很重要。如果计算网格划分得很细，即单元的尺寸很小，那么插值函数精度将会提高，方程组的解也就越精确。如果单元是满足收敛要求的，其近似解最后可收敛于精确解。当然，单元网格划分越密，其方程组个数也就越多，计算量越大，计算所需时间也就越长。
有限元分析的基本步骤大致可分为三个阶段：前期处理阶段、分析计算阶段和后处理阶段。前处理阶段的主要任务是将整体结构或其中一部分简化为理想的数学模型，用离散化的单元替代连续实体结构或求解区域；分析计算阶段是运用有限元法对结构离散模型进行分析计算；后处理阶段则是对计算结果进行分析、整理和归纳。
2.Mohr-Coulomb屈服准则
Mohr-Coulomb塑性模型主要适用于描述单调荷载下颗粒状材料在不同应力状态下屈服面的应力应变关系，作为岩土破坏的判断依据，在岩土工程中应用非常广泛。
Mohr-Coulomb模型屈服面函数为(www.xing528.com)
式中，φ是p-q应力面上Mohr-Coulomb屈服面的倾斜角，称为材料的摩擦角，0°≤φ≤90°；c是材料的黏聚力；Rmc（θ，φ）按式（4-2）计算，其控制了屈服面在平面π上的形状。
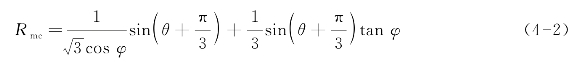
式中，θ是极偏角，定义为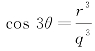
，其中，r为第三偏应力不变量J3。
图4-1给出了Mohr-Coulomb屈服面在子午面和平面π上的形状，由图可以比较其与Drucker-Prager屈服面、Mises屈服面以及Tresca屈服面之间的相对关系。
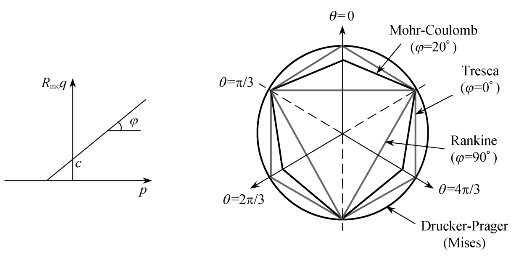
图4-1 Mohr-Coulomb模型中的屈服面
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
