地下工程对历史建筑的影响：灰色关联分析法

在客观世界中，因素之间的关系是比较复杂的，尤其是事物的表面现象和变化过程的随机性容易混淆人们的直觉，掩盖事物的本质，从而使人们在认识上得不到全面、可靠的信息，这样就难以对因素进行主次之分，在进行系统分析时也就遇到了困难，难以找到主要矛盾、发现主要特征和主要关系。灰色系统理论提供了一种崭新的多因素分析方法——灰色关联分析法。灰色关联是指事物间的不确定关联，或系统因子之间、因子对主行为之间的不确定关联。灰色关联分析是一种用灰色关联度顺序来描述因素间关系的强弱、大小、次序的方法，是通过灰色关联度来分析和确定系统因素间的影响程度或因素对系统主行为的贡献测度的一种方法。其基本思想是：以因素的数据序列为依据，用数学的方法研究因素间的几何对应关系，即序列曲线的几何形状越接近，则它们之间的灰色关联度越大，反之越小。灰色关联分析实际上也是动态指标的量化分析，充分体现了动态意义。

灰色关联分析是按事物的发展趋势作分析，因此对样本量的多少没有过多的要求，也不需要典型的分布规律，而且计算量比较小，其结果与定性分析结果会比较吻合，所以灰色关联分析法是一种具有独特优势、比较实用和可靠的分析方法。

3.5.1.1 基本概念

在进行关联分析之前，首先要选准反映系统特征行为的数据序列X0（有时也称为系统的参考序列），这个过程称为寻找系统行为映射量，用映射量间接地表征系统行为，如用（R&D经费/GDP）表征科技投入强度，用刑事案件发案率来反映社会治安面貌和社会秩序等。系统特征行为序列是系统分析中最为重要的因素，也是讨论的关键问题。确定了系统特征行为之后，将所讨论的问题通过语言模型定性分析，获得系统相关因素行为序列Xi（也称为比较序列）。这样就可以对系统进行关联分析了。下面给出X0和Xi的具体定义及其与灰色关联分析相关的一些基本概念。

定义1 设X0为表征系统行为的量，其在序号k上的观测数据为x0（k），k=1，2，…，n，则称X0（k）=（x0（1），x0（2），…，x0（n））为系统特征行为序列。

定义2 设Xi为系统因素，其在序号k上的观测数据为xi（k），k=1，2，…，n，则称Xi（k）=（xi（1），xi（2），…，xi（n））为系统的相关因素行为序列。

若k为时间序号，则Xi为行为时间序列，xi（k）为因素Xi在k时刻的观测数据；若k为指标序号，则Xi为行为指标序列，xi（k）为因素Xi关于第k个指标的观测数据；若k为观测对象序号，则Xi为行为横向序列，xi（k）为因素Xi关于第k个对象的观测数据。无论是时间序列数据、指标序列数据还是横向序列数据，都可以用作灰色关联分析。

定义3 设系统特征行为序列X0为增长序列，Xi为相关因素行为序列，则有

（1）当Xi为增长序列时，Xi与X0为正相关关系；

（2）当Xi为衰减序列时，Xi与X0为负相关关系。

定义4 设序列X=（x（1），x（2），…，x（n）），则称

（1）α=x（k）-x（k-1），k=2，3，…，n，为X在区间[k-1，k]上的斜率；

（2），s＞k，k=1，2，…，n-1，为X在区间[k，s]上的斜率。

3.5.1.2 数据变换及其性质

在进行关联分析之前，一般要对搜集来的原始数据进行数据变换和处理，因为所给的数据序列的取值单位一般来说是不同的，为保证模型建立的质量和系统分析结果的正确性，需要进行数据变换和处理，使其具有可比性。

1.单指标序列的数据变换及其性质

对单指标数据序列X=（x（1），x（2），…，x（n））进行无量纲的数据变换方法通常有以下几种。

（1）初值化变换，即

其中，x（k）d1=x（k）/x（1），x（1）≠0，k=1，2，…，n。

（2）均值化变换，即

其中，，k=1，2，…，n。

（3）极小化变换，即

其中，x（k）d3=x（k）/M，M≠0，k=1，2，…，n。

（4）极大化变换，即

其中，x（k）d4=x（k）/m，m≠0，k=1，2，…，n。

（5）极差化变换，即

其中，x（k）d5=（x（k）-m）/（M-m），M-m≠0，k=1，2，…，n。

（6）归一化变换，即

其中，x（k）d6=x（k）/x0，x0为大于零的某个常数，k=1，2，…，n。

（7）标准化变换，即

其中，x（k）d7=（x（k）-x-）/σ；σ≠0，k=1，2，…，n。

式中，x-为因素序列X的各个取值的样本均值，σ为样本标准差，M为因素序列X的最大值，m为序列X的最小值。

上述除了标准化变换d7外的各变换dj（j=1，2，…，6）都满足下面的性质。

对任意给定的非负单指标数据序列

有下面的性质：

（1）保号性：当x（k）＞0时，x（k）dj≥0。

（2）保序性：对∀x（k1），x（k2）∈X，当∀x（k1）＞x（k2）时，x（k1）dj＞x（k2）dj。

（3）保差异性：对∀x（k1），x（k2），x（k3），x（k4）∈X，

只对初值化变换进行证明，其他的几种变换同理可证。(www.xing528.com)

（1）当x（k）＞0，k=1，2，…，n时，。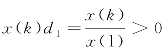

（2）对∀x（k1），x（k2）∈X，当∀x（k1）＞x（k2）时，，即x（k1）d1＞x（k2）d1。

（3）对∀x（k1），x（k2），x（k3），x（k4）∈X，

2.多指标序列的数据变化

设有指标序列

记M={i|i=1，2，…，m}为因素Xi的下标集合，N={k|k=1，2，…，n}为指标xi（j）的标号集合。

指标一般按其性质可以分为3种。①效益型（例如利润、产量）：指标值越大越好；②成本型：指标值越小越好；③固定型：指标值越接近某个固定值越好。因为指标的性质不同，所以对其实行数据变换也就有所不同。

（1）效益型指标变换

其中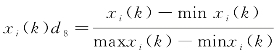，，i∈M，k∈N。

（2）成本型指标变换

其中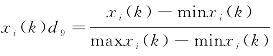，，i∈M，k∈N。

（3）固定型指标变换

其中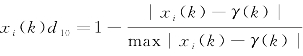，，i∈M，k∈N，γ（k）为关于指标k的固定值。

定义5 称D={Di|i=1，2，…，10}为灰色关联算子集。

定义6 设X为系统因素集合，D为灰色关联算子集，称（X，D）为灰色关联因子空间。

3.灰色关联公理与灰色关联度

为了建立一套完整的灰色关联理论体系，灰色关联四公理作为定义灰色关联度满足的条件被提出，即灰色关联分析模型是在灰色关联四公理的基础上来定义的。灰色关联四公理是指：

（1）规范性

（2）整体性

对于Xi，Xj∈X={Xs|s=0，1，2，…，m；m≥2}，有

（3）偶对对称性

对于Xi，Xj∈X，有

（4）接近性

其中，实数γ（X0，Xi）为X0与Xi的灰色关联度，γ（x0（k），xi（k））为X0与Xi在点k的灰色关联系数。

公理中的几个约束条件，是对关联度实质的一种体现，例如，整体性就体现了环境对灰色关联度的影响，环境不同，灰色关联度也随之变化。

4.参与灰色关联度计算的数据序列的可比性问题

在相互制约、相互激励的诸系统中，各系统间关系的密切程度可用表示各系统演变过程的序列间的关联度来表示。要比较两序列的相似性，若只考虑数值大小而忽略量纲，则比较的结果是无意义的，甚至会歪曲本质上的相似性。此时就要考虑数据序列的可比性问题。

按照灰色关联分析法的基本思想，要比较的实际上是各序列所描绘的曲线的几何形状的相似性。而如果要比较两个序列曲线的几何形状的相似程度，其前提应该是它们是可比的，即相比较的两个序列曲线应处于同一个参照坐标系中，这就要求两序列是具有同一个量纲的序列；相反，如果相比较的两序列具有不同的量纲，则它们就不能处于同一个参照坐标系中，也就无法对它们进行比较，此时这两个序列是不可比的。因此，在进行关联度计算前应首先判断数据序列的可比性。若数据序列为可比序列，则可以不进行数据变换处理，直接将数据代入量化模型进行计算。若数据序列为不可比序列，则必须进行数据变化处理。

总之，关联度量化模型是针对可比序列建立的，也就是说，当讨论一种关联度量化模型的各种优缺点时，应直接以可比序列为对象进行检验，这样才能从本质上说明一种量化模型的好坏。

5.灰色关联分析法的基本特征

（1）总体性

灰色关联度虽是数据序列几何形状的接近程度的度量，但它一般强调的是若干个数据序列对一个既定的数据序列接近的相对程度，即要排出关联度大小的顺序，这就是总体性，其将各因素统一置于系统之中进行比较与分析。

（2）非对称性

在同一系统中，甲对乙的关联度，并不等于乙对甲的关联度，这比较真实地反映了系统中因素之间真实的灰度关系。

（3）非唯一性

关联度随着参考序列不同、因素序列不同、原始数据处理方法不同、数据多少不同而不同。

（4）动态性

因素间的灰色关联度随着序列的长度不同而变化，表明系统在发展过程中，各因素之间的关联度也随着时间不断变化。