在专家调查法识别出风险因素的基础上，要进行风险评价，需构建一个合理的评价指标体系，充分考虑各风险因素之间的相互关系和影响。风险评价指标体系的设计直接关系到评价结果的客观性、准确性和有效性。
层次分析法（Analytical Hierarchy Process，AHP）是美国数学家A.L.Saaty在20世纪70年代提出的，是一种定性分析和定量分析相结合的方法，其在项目风险评价中运用灵活、易于理解，而且具有较高的精度。其评价的基本思路是：把复杂的风险问题分解为各个组成因素，将这些因素按支配关系分组形成有序的递阶层次结构，通过两两比较的方式确定层次中诸因素的相对重要性，然后综合判断以决定评价诸因素相对重要性的总顺序。层次分析法体现了决策思维的基本特征，即分解、判断、综合。运用层次分析法解决问题，大体可以分为以下四个步骤。
1.建立问题递阶层次结构
这是层次分析法中最重要的一步。首先，把复杂问题分解成元素，把这些元素按属性分成若干组，形成不同层次。同一层次的元素作为准则，对下一层次的某些元素起支配作用，同时它又受上一层次元素的支配。这种从上至下的支配关系形成了一个递阶层次。处于最上面的层次通常只有一个元素，一般是分析问题的预定目标或理想结果。中间的层次一般是准则、子准则，最低一层为基本风险因素。层次之间元素的支配关系不一定是完全的，即可以存在这样的元素，它并不支配下一层次的所有元素。
一个好的层次结构对解决问题是极为重要的。层次结构是建立在评价者对所面临的问题具有全面深入的认识基础上，如果在层次的划分和确定层次之间的支配关系上举棋不定，最好重新分析问题，弄清问题各部分之间的相互关系。
2.构造两两比较判断矩阵
在建立递阶层次结构以后，上下层次之间元素的隶属关系就被确定了。假定上一层次的元素Ck作为准则，对下一层次的元素A1，A2，…，An有支配关系，目的是在准则Ck之下按其相对重要性赋予A1，A2，…，An相应的权重。这一步中，要反复回答问题：针对准则Ck，两个元素Ai和Aj哪一个更重要，重要多少，并需要对重要多少赋予一定数值。
表3-4 两个因素重要性比较的量化结果
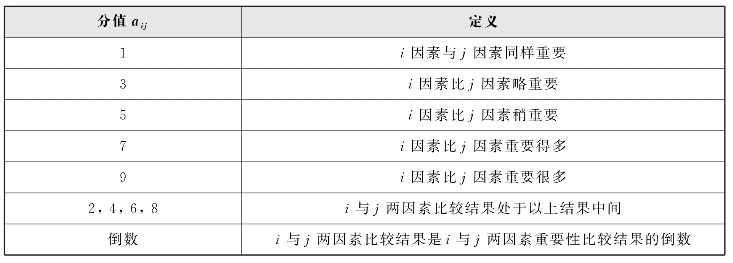
1～9的标度方法是将思维判断数量化的一种方法。首先，在区分事物的差别时，可以用相同、较强、强、很强、极端强的语言，再进一步细分，可以在相邻的两级中间插入折中的提法，因此对于大多数评价判断来说，1～9级的标度是适用的。其次，心理学的实验表明，大多数人对不同事物在相同属性上差别的分辨能力在5～9级之间，采用1～9的标度反映了多数人的判断能力。再次，当被比较的元素属性处于不同的数量级，一般需要将较高数量级的元素进一步分解，这样可以保证被比较元素在所考虑的属性上是同一个数量级或比较接近，从而适用于1～9的标度。在1～9的标度下，两个因素重要性比较的量化结果列于表3-4。对于n个元素来说，两两比较判断矩阵A为
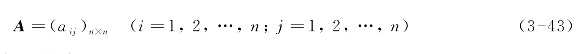
判断矩阵具有如下性质：
称A为正的互反矩阵。由于判断矩阵的性质，事实上，对于n阶判断矩阵仅需对其上（下）三角元素共n（n-1）/2个元素给出判断。矩阵A的元素不一定具有传递性，即未必成立等式
当式（3-45）成立时，则称矩阵A为一致性矩阵。在说明由判断矩阵导出元素排序权值时，一致性矩阵具有重要意义。
3.单一准则下元素的相对权重
这一步要解决在准则Ck下，n个元素A1，A2，…，An排序权重的计算问题，并进行一致性检验。对于A1，A2，…，An，通过两两比较得到判断矩阵A，求解特征根问题：
将所得到的特征向量w经正规化后作为元素A1，A2，…，An在准则Ck下的排序权重，这种方法称排序权向量计算的特征根方法。λmax存在且唯一，w可以由正分量组成，除了相差一个常数倍数外，w是唯一的。λmax和w的计算可采用幂法，步骤如下：
（1）设初值向量w0，可假定
（2）对于k=1，2，3，…，计算
式中，wk-1为经归一化所得到的向量。
（3）对于事先给定的计算精度，若
式中，wki表示wk的第i个分量。
式（3-49）成立则计算停止，否则继续计算新的
。(www.xing528.com)
（4）计算
在精度要求不高的情况下，可以用近似方法计算λmax和w，采用根法近似计算：
第一步，将A的元素按行相乘；
第二步，所得到的乘积分别开n次方；
第三步，将方根向量归一化，即得排序权向量w；
第四步，按式（3-52）计算λmax：
在判断矩阵的构造中，并不要求判断矩阵具有一致性，这是为客观事物的复杂性与人的认识多样性所决定的。但要求判断矩阵有大体的一致性却是必要的，例如，出现甲比乙极端重要，乙比丙极端重要，而丙比甲极端重要的情况一般是违反常识的。而且，当判断偏离一致性过大时，排序权向量计算结果作为评价依据将会出现问题。因此在得到λmax后，需要进行一致性检验，步骤如下：
（1）计算一致性指标CI
式中，n为判断矩阵的阶数。
平均随机一致性指标RI是多次（500次以上）重复进行随机判断矩阵特征值的计算之后取算术平均值得到的。1～15阶重复计算1 000次的平均随机一致性指标如表3-5所列。
表3-5 平均随机一致性指标
（2）计算一致性比例CR
若CR＜0.1，则认为判断矩阵的一致性是可以接受的。
4.各层元素的组合权重
为了得到递阶层次结构中每一层次中所有元素相对于总目标的相对权重，需要把第3步的计算结果进行适当的组合，并进行总的判断矩阵一致性检验。这一步骤是由上而下逐层进行的。
假定已经计算出第（k-1）层元素相对于总目标的组合排序权重向量。
，第k层在第（k-1）层第j个元素作为准则下元素的排序权重向量为
，其中不受支配[即与（k-1）层第j个元素无关]的元素权重为零。令
，则第k层n个元素相对于总目标的组合排序权重向量为
更一般地，有排序的组合权重公式：
式中，a2为第2层次元素的排序向量，3≤k≤h，h为层次数。
对递阶层次组合判断的一致性检验，需要类似地逐层计算CI。若分别得到了第（k-1）层的计算结果CI，RI和CR，则第k层的相应指标为
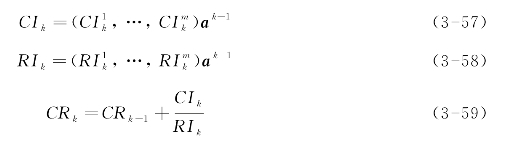
式中，
分别为在第（k-1）层第i个准则下判断矩阵的一致性指标和平均随机一致性指标。当CRk＜0.1时，认为递阶层次在第k层上的整个判断有较好的一致性。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
