人工神经网络预测历史建筑沉降应用效果

基坑开挖往往会引起邻近历史建筑物产生沉降，所以基坑开挖之前需要对邻近历史建筑物沉降进行预测，人工神经网络是一种有效的预测方法。神经网络是人类在认识自身并对生物神经网络进行模拟的基础上而产生的一门智能仿生技术，由于其具有强大的学习能力和非线性映射能力，所以随着计算机和人工智能的发展与广泛应用而获得巨大生命力。神经网络技术应用到岩土工程领域，对岩土的离散性、不确定性进行研究，已经取得了很大的进展。

1.基本原理

神经网络技术具有很好的非线性映射能力，相比于线性相关法、经验公式法等有着较大的优越性。它利用自身优势自主学习训练，综合各方面因素及其之间的影响给出输出值，在岩土工程领域中，有着广阔的应用前景。在神经网络的设计和应用过程中，根据神经网络的互联结构，分为五种典型的结构：前馈网络、输入输出有反馈的前馈网络、前馈内层互联网络、反馈型全互联网络、反馈型局部连接网络等。

多层前馈性神经网络是根据信号的传播方向决定的，其信号向前传递，而误差反向传播。当正向传播时，信息从输入层进入，经过隐含单元层处理后传向输出层，每一层只会影响下一层的神经单元状态。假如得到的输出值和期望值相差较大，网络就自动转入反向传播，从而根据预测的误差值来调整网络阈值和权值，使神经网络的输出值和期望值相接近。图3-16所示是三层神经网络的拓扑结构。

图3-16　三层神经网络拓扑结构

i—输入端点序号；h—隐藏层节点序号；j—输出层节点序号；—第k次第i节点输入信号；—第k次第h节点输出信号；—第k次第j节点输出信号；k—训练对序号；Wih—输入隐蔽层节点的权值；Whj—隐蔽层节点至输出层节点的权值。

神经网络训练算法是调节每层的权值，从而使网络对各个训练组进行适应，该训练组是根据输入/输出对相互形成的。根据训练过程，添加第k个输入层时，使得隐蔽层第h节点相应输入权值为

对应点相应输出为

输出层第j节点输入加权总和为

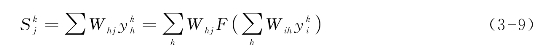
对应的最后输出为

采用“δ规则”训练算法：

或

利用“优化梯度下降法”，隐藏层至输出层的连接加权调节量为

式中，为输出节点的误差信号。

输入层至隐藏层权值修正为ΔWhj，同时考虑E（W）对ΔWhj求导

根据分层链导法可得

其中，

而

(www.xing528.com)

式中，为输出节点误差信号为隐藏节点误差信号。

有着相同的形式，但它们的误差值定义有所不同，因此该算法对任意一层的权值修正为

式中，δ0为端点的输出误差；yin为任意层的实际输入值。

当δ0为实际输出层时

当δ0为实际隐藏层时

神经网络算法的转移函数通常采用S型函数，其导数为

其相应输出层的误差为

2.算法步骤

根据神经网络相关知识，假设该网络一共有m层，那么就表示第m层中对应的第j节点的输出值，因此表示第0层第j节点的输出值，即xj。

（1）在各个权值中选择最小的值。

（2）根据要求选择数据对（xk，Tk），使k∈（1，2，…，m），将输入向量施加到输入层：

（3）根据关系式

式中，为隐藏层第j节点的输入权值。

通过网络使信号向前传播，分别计算每一层的输出值，直到最后一层。

（4）计算输出层各个节点的误差值

（5）通过反向传播，得出每层节点的误差

式中，m=m，m-1，…，1，最终计算出每层各个节点的误差值。

（6）根据公式

式中，η为训练速率系数，η∈[0.001，1]。从而有：

（7）返回至步骤（2），再根据步骤（2）—（7）输入下一组数据，直至训练完所有数据组，并且输出值和目标函数相等为止。